如何判断一个链表是否存在环
哈希表法
哈希表法的基本思路是:把访问过的结点记录下来,如果在遍历中遇到了访问过的结点,那么可以确定链表中存在环。记录访问过的结点,最常用的方法就是使用哈希表了。
有了这一点思路之后,我们很快可以写出相应的题解代码:
public boolean hasCycle(ListNode head) {
// 记录已访问过的结点
Set<ListNode> seen = new HashSet<>();
for (ListNode q = head; q != null; q = q.next) {
if (seen.contains(q)) {
// 遇到已访问过的结点,确定链表存在环
return true;
}
seen.add(q);
}
// 遍历循环正常退出,链表不存在环
return false;
}
快慢指针法
我们让快指针一次前进两个结点,慢指针一次前进一个结点。当快慢指针都进入环路时,快指针会将慢指针「套圈」,从后面追上慢指针,如下图所示。
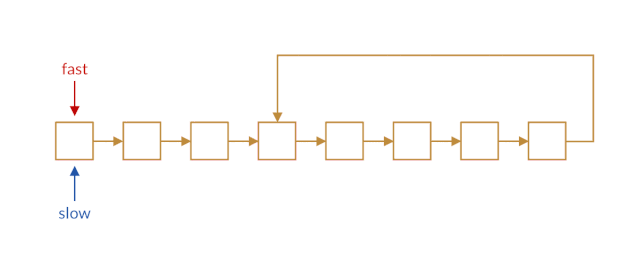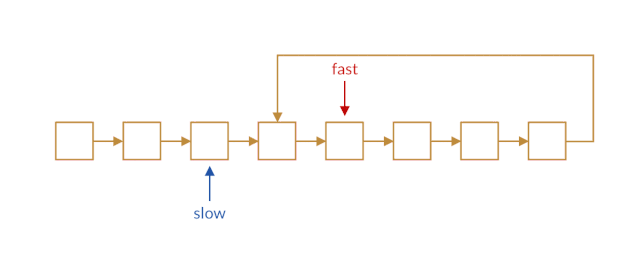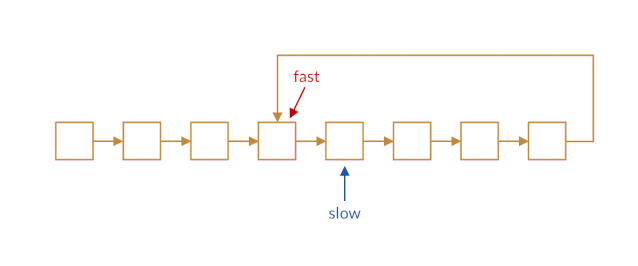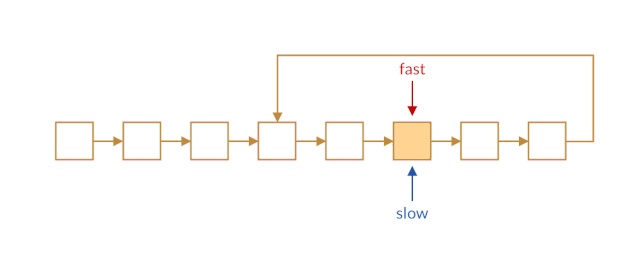
这样,如果快指针追上了慢指针,我们就可以判断链表中存在环路。而如果链表中不存在环的话,快指针会永远走在慢指针的前面,它们不会相遇,且快指针最终将到达链表末尾。
依照这个思路,我们可以写出以下的题解代码。
public boolean hasCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
// fast 和 slow 指向同一个结点,说明存在“套圈”
if (fast == slow) {
return true;
}
}
// fast 到达链表尾部,则不存在环
return false;
}
寻找环的入口结点
如果用哈希表的方法,这道题其实和前一题是一样的,没什么难度。
链表分为两段:无环段和有环段。我们设无环段的长度为(a),环的长度为(b) 。当快慢指针相遇时,我们设慢指针已经走了(x)步,那么快指针这时候已经走了$ 2x $步。快指针套圈了慢指针,也就是比慢指针多走了若干圈。我们可以列出公式:
[2x-x=kb
]
其中,(k)可以是任意正整数,因为快指针可能套了慢指针不止一圈。将上式化简得到:
[x=kb
]
这个(x)恰好是慢指针走的步数。也就是说,慢指针目前前进的(x)步,正好是环的长度(b)的整数倍。
那么,慢指针再走(a)步,就可以正好到达环的起点。这是因为,(x+a=a+kb) ,正好够从链表头部出发,走一段无环段((a)),再把有环段走(k)圈((kb))。
如果我们在此时再用一个指针 q 从链表头部出发。那么指针 q 和慢指针 slow 会在走了(a)步以后恰好在环的起点处相遇。这样,我们就可以知道环的起点了。
根据以上思路,我们可以写出下面的题解代码:
public ListNode detectCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
// 快慢指针相遇,说明链表存在环
if (fast == slow) {
// 此时 slow 指针距离环的起点的距离恰好为 a
ListNode q = head;
while (q != slow) {
slow = slow.next;
q = q.next;
}
// slow 和 q 相遇的位置一定是环的起点
return slow;
}
}
// 链表不存在环,返回 null
return null;
}