Deep Learning 的阅读笔记（一）

1. 什么叫做矩阵分解？

满足于 Av = λv ，矩阵分解又分为：特征分解和奇异值分解

特征分解：只限于方征，Av = λv 其中的 v 是 矩阵 A 的特征向量，如果公式成立的话，那么 λ 就是对应的特征值，每个矩阵不只含有唯一的特征向量和对应的特征值。

奇异值分解：任何矩阵，常用于个性化推荐、PCA 降维和 NLP，公式为 A = U∑V^T ，其中  是一个  的矩阵，  是一个  的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，  是一个  的矩阵。

如何求解 U,Σ,V这三个矩阵

如果我们将A的转置和A做矩阵乘法，那么会得到n×n的一个方阵  。既然  是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

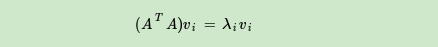
这样我们就可以得到矩阵  的n个特征值和对应的n个特征向量v了。将  的所有特征向量张成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

如果我们将A和A的转置做矩阵乘法，那么会得到m×m的一个方阵  。既然  是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

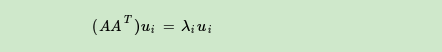
这样我们就可以得到矩阵  的m个特征值和对应的m个特征向量u了。将  的所有特征向量张成一个m×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

U和V我们都求出来了，现在就剩下奇异值矩阵Σ没有求出了.

由于Σ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ就可以了。

我们注意到:

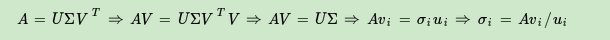
这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵Σ。

上面还有一个问题没有讲，就是我们说  的特征向量组成的就是我们SVD中的V矩阵，而

 的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。

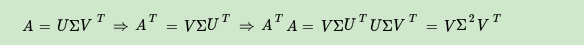
上式证明使用了  。可以看出  的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到  的特征向量组成的就是我们SVD中的U矩阵。

进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：

这样也就是说，我们可以不用  来计算奇异值，也可以通过求出  的特征值取平方根来求奇异值。

SVD 常用于推荐算法，数据降维和降噪，实现并行化