[codeforces821E]Okabe and El Psy Kongroo

题意：(0,0)走到(k,0),每一部分有一条线段作为上界，求方案数。

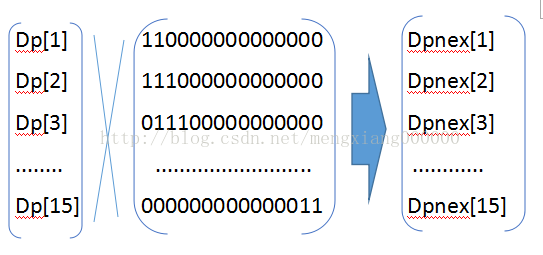
解题关键：dp+矩阵快速幂，盗个图，注意ll

关于那条语句为什么不加也可以，因为我的矩阵C，就是因为多传了了len的原因，其他位置都是0，所以不需要加

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<iostream>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
struct mat{
    ll m[17][17];
}A;

mat mul(mat &A,mat &B,ll len){
    mat C={0};
    for(int i=0;i<=len;i++){
        for(int k=0;k<=len;k++){
            for(int j=0;j<=len;j++){
                C.m[i][j]=(C.m[i][j]+A.m[i][k]*B.m[k][j]%mod+mod)%mod;
            }
        }
    }
    return C;
}

mat mod_pow(mat A,ll n,ll len){
    mat B={0};
    for(int i=0;i<=len;i++) B.m[i][i]=1;
    while(n>0){
        if(n&1) B=mul(B,A,len);
        A=mul(A,A,len);
        n>>=1;
    }
    return B;
}

int main(){
    ll n,k;
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    for(int i=0;i<16;i++){
        int j=i-1>=0?i-1:0;
        for(;j<=i+1&&j<16;j++){
            A.m[i][j]=1;
        }
    }
    mat C;
    cin>>n>>k;
    mat B={0};
    B.m[0][0]=1;
    ll cnt=0;
    for(int i=0;i<n&&cnt<k;i++){
        ll a,b,c;
        cin>>a>>b>>c;
        if(b>k) b=k;
        cnt+=b-a;
        C=mod_pow(A, b-a, c);
        B=mul(B, C, c);
        for(ll j=c+1;j<16;j++) B.m[j][0]=0;//这句话不加也可以，为什么？
    }
    cout<<(B.m[0][0]+mod)%mod<<"
";
    return 0;
}