数学之美：判断两个随机信号序列相似度

[导读] 在工程应用时，有时候需要计算两个信号序列的相似度，实际信号由于在采集过程中会混入干扰，如果简单的依次比较各样本是否相等或者差值，则很难判定两个信号序列的相似程度。本文来聊聊我的一些思路。

什么是互相关函数？

在统计学中，相关是描述两个随机变量序列或二元数据之间的统计关系，无论是否具有因果关系。广义上讲，相关性是统计上的关联程度，它通常指的是两个变量的线性相关的程度。比如商品的价格和消费者购买愿意数量之间的关系，也即所谓的需求曲线。

相关性是有用的，因为它们可以描述一种可在实践中加以利用的预测作用。例如，根据电力需求和天气之间的相关性，电力公司可能会在天气凉快时候生产更少的电力。在这个例子中，有一定的因果关系存在，因为极端天气导致人们使用更多的电力用于取暖或制冷。然而，一般而言，相关性的存在并不足以推断出因果关系的存在，也就是说相关性并不意味着因果关系。

连续信号里，为函数及的互相关函数定义为：
$${\rho }_{xy}={\int }_{-\infty }^{\infty }{f}_x(t)f_y(t-\tau )dt$$

离散信号,假设两个信号序列x(n)及y(n)，每个序列的能量都是有限能量序列，则x(n)及y(n)的互相关序列为：
$${\rho }_{xy}=\sum _{-\infty }^{\infty }x(n)y(n-l)$$
那么互相关函数就是描述在连续信号或离散序列的相关程度的一种统计度量。

什么是相关系数？

最熟悉的度量两个量之间的相关性的方法是皮尔逊乘积矩相关系数(PPMCC)，也称为“皮尔逊相关系数”，通常简称为“相关系数”。在数学上，它被定义为对原始数据的最小二乘拟合的质量（拟合程度或效果）。它是由数据集两个变量的协方差的比率，归一化到他们的方差的平方根得到的。数学上，两个变量的协方差除以标准差的乘积。

皮尔逊积矩相关系数试图通过两个随机序列的数据集建立一条最佳拟合曲线，实质上是通过列出期望和由此产生的皮尔逊相关系数表明实际数据集离预期值有多远。根据皮尔逊相关系数的符号，如果数据集的变量之间存在某种关系，可以得到负相关或正相关。其定义公式如下：
$${\rho }_{xy}=corr(X,Y)=\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}$$
上述公式展开为：
$${\rho }_{xy}=\frac{E[(X-\overline{X})(Y-\overline{Y})]}{{\sigma }_X{\sigma }_Y}$$
在根据期望计算公式展开，就得到：
$${\rho }_{xy}=\frac{{\sum }_{i=1}^n[x(i)-\overline{x}]\ast [y(i)-\overline{y}]}{\sqrt{{\sum }_{i=1}^n[x(i)-\overline{x}{]}^2}\sqrt{{\sum }_{i=1}^n[y(i)-\overline{y}{]}^2}}$$
如果考察延迟d处的互相关${\rho }_{xy}$,则上述公式就变为:
$${\rho }_{xy}=\frac{{\sum }_{i=1}^n[x(i)-\overline{x}]\ast [y(i-d)-\overline{y}]}{\sqrt{{\sum }_{i=1}^n[x(i)-\overline{x}{]}^2}\sqrt{{\sum }_{i=1}^n[y(i-d)-\overline{y}{]}^2}}$$
为了方便理解，本文就不考察延迟节拍了。

相关系数有啥用？

皮尔逊相关系数的绝对值不大于1是Cauchy–Schwarz不等式的推论（有兴趣的可以去找书看看）。因此，相关系数的值在[-1,1]之间。在理想的增加线性相关关系情况下，相关系数为+1；在理想的减少（反相关）线性关系情况下，相关系数为-1；在所有其他取值情况下，表示变量之间的线性相关程度。当它接近零时，更接近于不相关。系数越接近-1或1，变量之间的相关性越强。

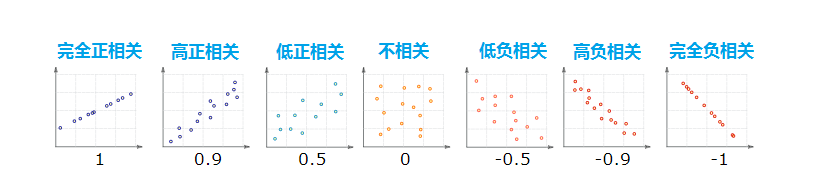
故，相关系数其值范围分布在区间[-1,1]：

• 1表示完全正相关
• 0表示不相关
• -1表示完全负相关

为了方便理解，假定两个随机序列按照下面各类情况分布，下面的数字为相关系数：

程序如何实现呢？

上述公式在实际编程时，当然可以直接按照公式编制代码，如果仔细观察会发现该公式可以进一步简化，过程省略：
$${\rho }_{xy}=\frac{n\sum x_i{y}_i-\sum x_i\sum y_i}{\sqrt{[n\sum x_i^2-(\sum x_i{)}^2][n\sum y_i^2-(\sum y_i{)}^2]}}$$
由这个公式就很容易编程了，干货在这里，可以拿去稍加改造即可使用:

#include <stdio.h>
#include <math.h>

/* 返回值在区间： [-1,1]          */
/* 如返回-10，则证明输入参数无效    */
#define delta 0.0001f
double calculate_corss_correlation(double *s1, double *s2,int n)
{
    double sum_s12 = 0.0;
    double sum_s1  = 0.0;
    double sum_s2  = 0.0;
    double sum_s1s1 = 0.0; //s1^2
    double sum_s2s2 = 0.0; //s2^2
    double pxy = 0.0;
    double temp1 = 0.0;
    double temp2 = 0.0;
    
    if( s1==NULL || s2==NULL || n<=0)
      return -10;
    
    for(int i=0;i<n;i++)
    {
         sum_s12  += s1[i]*s2[i];
         sum_s1   += s1[i];
         sum_s2   += s2[i];
         sum_s1s1 += s1[i]*s1[i]; 
         sum_s2s2 += s2[i]*s2[i]; 
    }
    
    temp1 = n*sum_s1s1-sum_s1*sum_s1;
    temp2 = n*sum_s2s2-sum_s2*sum_s2;
    
    /* 分母不可为0 */
    if( (temp1>-delta && temp1<delta) || 
        (temp2>-delta && temp2<delta) ||
        (temp1*temp2<=0) )
    {
        return -10;  
    }       
    
    pxy = (n*sum_s12-sum_s1*sum_s2)/sqrt(temp1*temp2);
    
    return pxy;
}
double s1[30] = {
0.309016989,0.587785244,0.809016985,0.95105651,1,0.951056526,
0.809017016,0.587785287,0.30901704,5.35898E-08,0,0,
0,0,0,0,0,0,
0,0,0,0,0,0,
0,0,0,0,0,0
};
double s2[30] = {
0.343282816,0.686491368,0.874624132,0.99459642,1.008448609,
1.014252458,0.884609221,0.677632906,0.378334666,0.077878732,
0.050711886,0.066417083,0.088759401,0.005440732,0.04225661,
0.035349939,0.0631196,0.007566056,0.053183895,0.073143706,
0.080285063,0.030110227,0.044781145,0.01875573,0.08373928,
0.04550342,0.038880858,0.040611891,0.046116826,0.087670453
};

int main(void)
{
    double pxy;
    double s3[30];

    pxy = calculate_corss_correlation(s1,s2,30);
    printf("pxy of s1 and s2:%f
",pxy);  
    
    pxy = calculate_corss_correlation(s1,s1,30);
    printf("pxy of s1 and s1:%f
",pxy);  

    for(int i=0;i<n;i++)
    {
        s3[i] = -1*s1[i];
    }
    pxy = calculate_corss_correlation(s1,s3,30);
    printf("pxy of s1 and s3:%f
",pxy);  
    
    return 0;
}

运行结果为：

pxy of s1 and s2:0.997435
pxy of s1 and s1:1.000000
pxy of s1 and s1:-1.000000

将这三个信号绘制成波形来看看：

由图看出：

• S1与S2非常相似，其相关系数为0.997435，高度相似
• S1与-S1则刚好相位相反，理想反相关，其相关系数为-1
• S1与S1则理所当然是一样的，其相关系数为1

再来一组信号对比一下：

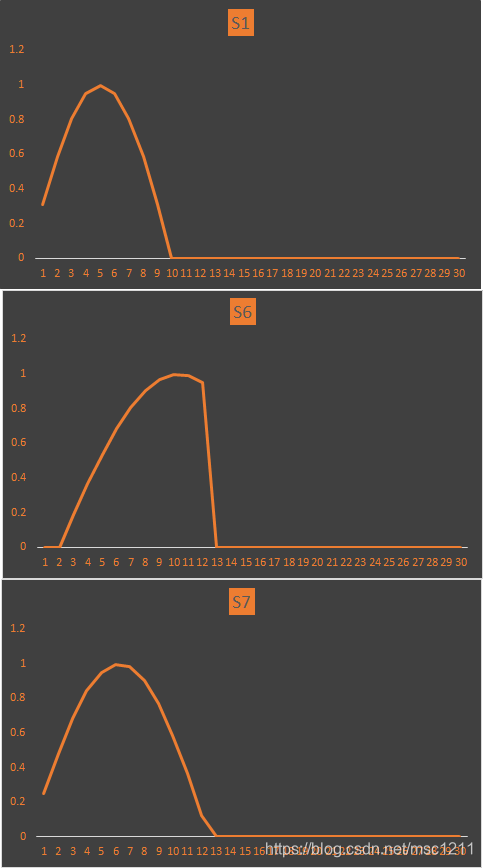
其波形数据为：

double s1[30]={
    0.309016989,0.587785244,0.809016985,0.95105651,1,
    0.951056526,0.809017016,0.587785287,0.30901704,5.35898E-08,
    0,0,0,0,0,
    0,0,0,0,0,
    0,0,0,0,0,
    0,0,0,0,0
};
double s6[30]={
    0,0,0.187381311,0.368124547,0.535826787,
    0.684547097,0.809016985,0.904827044,0.968583156,0.998026727,
    0.992114705,0.951056526,0,0,0,
    0,0,0,0,0,
    0,0,0,0,0,
    0,0,0,0,0
};
double s7[30]={
    0.187381311,0.368124547,0.535826787,0.684547097,0.809016985,
    0.904827044,0.968583156,0.998026727,0.992114705,0.951056526,
    0.876306697,0.770513267,0.637424022,0.481753714,0,
    0,0,0,0,0,
    0,0,0,0,0,
    0,0,0,0,0
};

测试计算其相关系数：

pxy of s1 and s6:0.402428
pxy of s1 and s7:0.612618

可见，S6、S7与S1的相关系数越来越大，从波形上看相似度也越来越大。

总结一下

通过相关系数可以比较完美的判断两个信号序列，或者两个随机变量之间的相似度。相关系数以及互相关函数应用很广，本文仅仅描述了一个工程上应用较多的实际栗子。事实上，该数学特性有着广泛的应用，有兴趣的可以深度学习探讨一下。