"遍历"是二叉树各种操作的基础,可以在遍历过程中对结点进行各种操作,如:对于一棵已知树可求结点的双亲,求结点的孩子结点,判定结点所在的层次等,反之也可在遍历二叉树的过程中生成结点,建立二叉树的存储结构
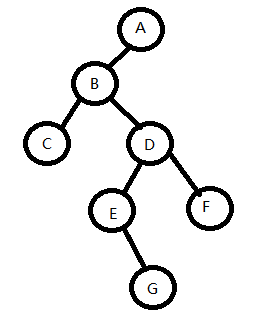
按先序序列建立二叉树的二叉链表的过程:
ABC##DE#G##F###(#代表空)
void CreateBiTree(BiTree &T) { char ch; scanf("%c",&ch); if(ch == '#') T = NULL; else{ if(!(T = (BiTNode *)malloc(sizeof(BiTNode)))) exit(OVERFLOW);//OVERFLOW:-1 T->data = ch;//生成根结点 CreateBiTree(T->lchild); CreateBiTree(T->rchild); } }
//中序、后序、类似可得
遍历二叉树的基本操作是访问结点,则不论按哪一种次序进行遍历,对含n个结点的二叉树,其时间复杂度均为O(n),所需辅助空间为遍历过程中栈的最大容量,即树的深度,最坏情况下为n,则空间复杂度也为O(n)