用循环链表求解约瑟夫问题

　　约瑟夫问题的提法：n个人围成一个圆圈，首先第1个人从1开始，一个人一个人的顺时针报数，报到第m个人，令其出列；然后再从下一个人开始，从1顺时针报数，报到第m个人，再令其出列，…，如此下去，直到圆圈中只剩一个人为止，此人即为优胜者。

　　例如  n = 8   m = 3   

　　

　　

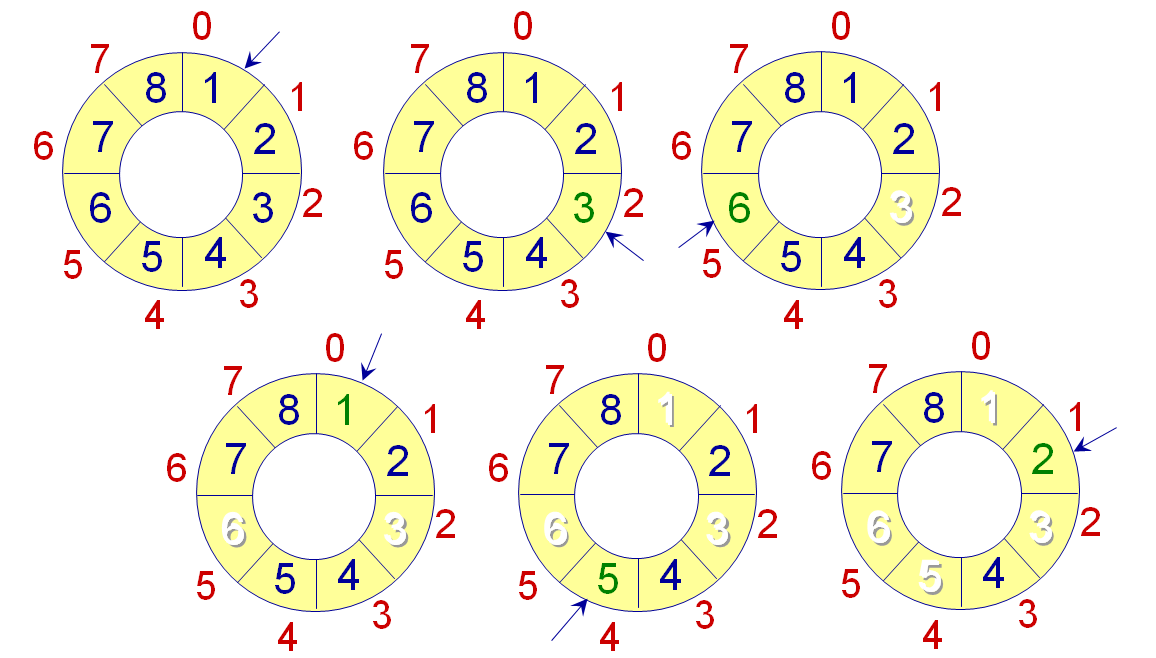
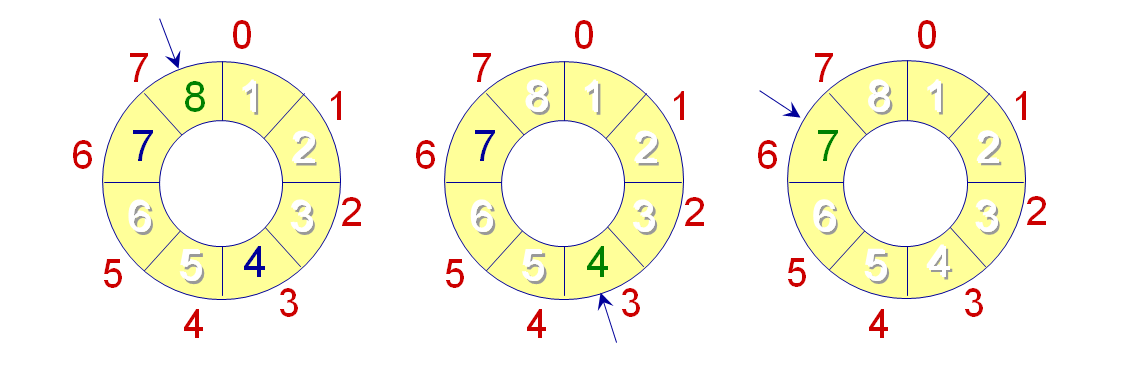
　　该问题老师让我们在带头节点的单循环链表，不带头节点的单循环链表，双向循环链表，静态循环链表中四选其一实现，我看到问题后第一反应选了带头节点单循环链表，以为这样可以统一空表和非空表的操作，事实上在这个问题中并不需要考虑这些，不过好在四种方式实现起来差不多。

　　这里给出我用带头节点的单循环链表求解约瑟夫问题的源码：

#include <iostream>
using namespace std;

template <class T>
struct CircLinkNode            // 循环链表结点定义
{
    T data;                    // 数据域
    CircLinkNode<T>* link;    // 指针域
    CircLinkNode(CircLinkNode<T>* ptr = NULL)    // 无参构造函数(带默认参数)
    {
        link = ptr;
    }
    CircLinkNode(T d, CircLinkNode<T>* ptr = NULL)
    {
        data = d;
        link = ptr;
    }
};

template <class T>
class CircList     // 循环链表类定义
{
private:
    CircLinkNode<T>* first;                // 头指针
public:
    CircList()                            // 构造函数
    {
        first = new CircLinkNode<T>(0);    // 附加头结点的值为0
        first->link = first;            // 循环链表最后一个结点要指向头结点
    }
    CircLinkNode<T>* Locate(int i);        // 定位第i个结点
    bool Insert(int i, T x);            // 在第i个结点后插入x
};

template<class T>
CircLinkNode<T>* CircList<T>::Locate(int i)    // 定位第i个结点
{
    if (i < 0)                            // i值不合理
        return NULL;
    if (i == 0)                            // 定位的是头结点         
        return first;
    CircLinkNode<T>* current = first;
    if (current->link == first)            // 循环链表为空
        return NULL;
    int count = 0;
    while (count < i)                    // 偱链找第i个结点
    {
        current = current->link;
        if (current != first)            // 计数规避附加头结点
        {
            count++;
        }
    }
    return current;
}

template<class T>
bool CircList<T>::Insert(int i, T x)    // 在第i个结点后插入新结点
{
    CircLinkNode<T>* current = Locate(i);
    if (current == NULL)
        return false;                    // 插入不成功
    CircLinkNode<T>* newNode = new CircLinkNode<T>(x);
    if (newNode == NULL)
    {
        cerr << "存储分配错误!" << endl;
        exit(1);
    }
    newNode->link = current->link;
    current->link = newNode;
    return true;                        // 插入成功
}


template <class T>
void Josephus(CircList<T>& Js, int n, int m)
{
    CircLinkNode<T> *p = Js.Locate(1);// p初始化指向第一个人
    CircLinkNode<T>    *pre = NULL;    
    for (int i = 1; i < n; i++) // 执行n-1次
    {
        for (int j = 1; j < m; j++) // 数m-1个人
        {    
            pre = p;
            p = p->link;
            if (p == Js.Locate(0))  // 计数忽略附加头结点
            {
                j--;
            }
        }
        cout <<"第"<<i<< "轮出列的人是" << p->data << endl;
        pre->link = p->link;
        delete p;     
        p = pre->link;
        if (p == Js.Locate(0))
            p = p->link;
    }
    cout << "最后的优胜者是" << p->data << endl;
};

int main()
{
    CircList<int> clist;        // 建立带头结点的单循环链表
    int person_num, cycle;
    cout << "输入游戏者人数和报数间隔 : ";
    cin >> person_num >> cycle;
    for (int i = 1; i <= person_num; i++)
        clist.Insert(i - 1, i);            // 建立约瑟夫环    
    Josephus(clist, person_num, cycle); // 解决约瑟夫问题

    return 0;
}

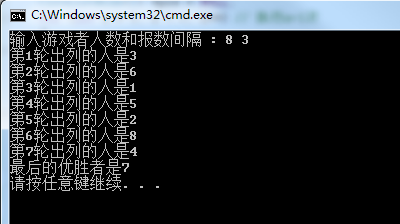
　　程序的运行结果如下：