并查集
并查集(Union-Find Sets)是一种非常精巧而实用的集合,集合中的每个元素仍是一个集合,即它是集合的集合。在并查集中的元素(集合)内部进行查找操作以及并查集中的元素(集合)之间的合并操作的时间复杂度均可视为O(1),它主要用于处理一些不相交集合的合并问题,在合并之前,需要先判断两个元素是否属于同一集合,这就需要用查找操作来实现,即先查找后合并。
并查集的原理也比较简单,逻辑上使用树来表示集合,树的每个节点就表示集合中的一个元素,指针指向其直接父节点,根结点对应的元素就是该集合的“代表”,指针指向自己,沿着每个节点的指针不断向上查找,最终就可以找到该树的根节点,即该集合的代表元素。如下图所示。

上图有两个集合,其中第一个集合为 {a,b,c,d},代表元素是 a;第二个集合为 {e,f,g},代表元素是 e,它们整体是一个并查集 { {a,b,c,d}, {e,f,g} }。
假设使用一个足够长的数组来存储集合元素,并查集在初始化时构造出下图的森林,其中每个元素都是一个单元素集合,即父节点是其自身:

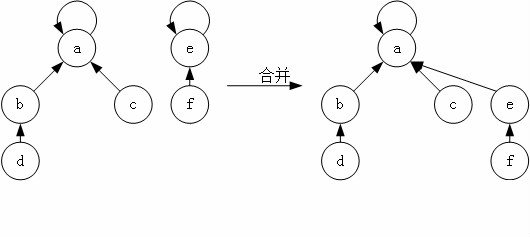
并查集内的合并操作非常简单,就是将一个集合的树根指向另一个集合的树根。这里可以应用一个简单的启发式策略——按秩合并。该方法使用秩来表示树高度的上界,在合并时,总是将具有较小秩的树根指向具有较大秩的树根。简单的说,就是总是将较矮的树作为子树,添加到较高的树中。如下图所示,第一个集合为 {a,b,c,d},代表元素是 a,秩为3;第二个集合为 {e,f},代表元素是 e,秩为2;合并两个集合得到集合 {a,b,c,d,e,f},代表元素是 a,秩为3。
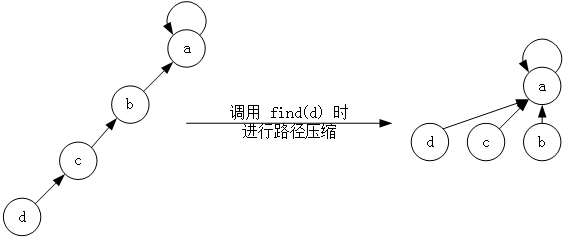
对于并查集内的查找操作,其目的就是找到所在集合的代表元素,如果每次都沿着父节点向上查找,那时间复杂度就是树的高度,完全不可能达到常数级。这里需要应用另一种简单有效的启发式策略——路径压缩。在每次查找时,令查找路径上的每个节点都直接指向我们要找的根节点,如下图所示。
关于并查集,一些常见的用途有求连通子图(判断连通性)、求最小生成树的 Kruskal 算法和求最近公共祖先(Least Common Ancestors, LCA)等。
习题:畅通工程
题目来源:HDOJ-1232-畅通工程
首先在地图上给你若干个城镇,这些城镇都可以看作点,然后告诉你哪些对城镇之间是有道路直接相连的。最后要解决的是整幅图的连通性问题。比如随意给你两个点,让你判断它们是否连通,或者问你整幅图一共有几个连通分支,也就是被分成了几个相互独立的连通子图。像畅通工程这题,问还需要修几条路,实质就是求有几个连通分支。如果有1个连通分支,说明整幅图上的点都连起来了,不需要再修路了;如果有2个连通分支,则只需要再修1条路,从两个连通分支中各选一个点,把它们连起来,那么所有的点都连起来了;如果有3个连通分支,则只需要再修两条路……
源码如下:
#include<iostream> using namespace std; const int CMAX = 1001; // 最多1000个城镇(编号从1开始) int parent[CMAX]; // 存放各结点的直接父节点,对于根结点,parent指向本身 int Rank[CMAX]; // 存放各结点的秩,即该结点在子树中的高度(实际上只有根结点的秩在按秩合并时才有价值) int Find(int x) // 带有路径压缩的查找过程,返回根结点(代表元素) { if (x != parent[x]) parent[x] = Find(parent[x]);// 沿着查找路径递归向上直到找到根 return parent[x]; // 找到根,开始回溯,进行路径压缩 } void Union(int x, int y) // 按秩合并两个树(集合),让具有较小秩的根指向具有较大秩的根 { int root1 = Find(x); int root2 = Find(y); if (root1 == root2) // 根结点相同,无需合并 return; if (Rank[root1] < Rank[root2]) { parent[root1] = root2; } else { parent[root2] = root1; if (Rank[root1] == Rank[root2]) // 只有秩相等时需要递增根的秩(大树合并小树,根秩不变) Rank[root1]++; } } int main() { int N, M; // 城镇数目和道路数目 while (scanf("%d%d", &N, &M) && N) // 当N为0时,输入结束 { int tree_num = 0; // 树的个数,即连通分支数 for (int i = 1; i <= N; i++) // 初始化每个结点独自成树,秩为1 { parent[i] = i; Rank[i] = 1; } int city1, city2; for (int i = 1; i <= M; i++) // 读取M条道路,合并连通的城镇 { scanf("%d%d", &city1, &city2); Union(city1, city2); } for (int i = 1; i <= N; i++) { if (parent[i] == i) // 每找到一个根就有一个连通分支 tree_num++; } printf("%d ", tree_num - 1); // 把这些连通分支连起来需要修tree_num-1条路 } return 0; }
提交结果:
参考资料: 《算法导论第3版》—— 21.3 不相交集合森林