修改code completion快捷键位CTRL+ENTER,帮助提示函数名称
修改命令行提示符的属性,开启快速编辑模式,方便调试
添加c++11语言标准支持
开启代码调试功能
对输入的字符串进行切割时,可以使用scanf按照指定格式分别输入达到切割效果,比如:
//对于这样的输入
3-10 99
11-5 87
102-1 0
//对于这种格式不绝对统一的字符串,可以自己构造相应的scanf分割对应的数据
scanf("%d-%d %d", &t, &num, &score);
对于需要进行除法运算的变量,并且有精确度要求的时候,可以这样
double grade =0;
//其中fullscore数组为int类型,在*1.0小数之后,自动转换为浮点型
grade += fullscore[j] * 1.0 / 2;
//或者这样强转
grade += (double)fullscore[j]/2;
如果在getline读取行之前还有其它的输入字符(不管是字符还是整数),则需要保证在调用getline函数之前,使用getchar()函数读取一次回车符,然后再调用
#include<iostream>
using namespace std;
int main() {
char n;
scanf("%c",&n);
getchar();
string str;
getline(cin,str);
cout<<str;
}
散列表的应用:在需要进行遍历数组内容,判断某一个元素是否存在时,可以使用一个大数组,初始化为0,录入数据时,相应数据(把下标看成数据)的内容修改为1,这样判断的时候直接判断a[element]==1即可,其中element为录入的数据。这样就把O(n)级别的时间复杂度降到了O(1)
atoi&stoi(stol)&strtol区别
即使不记得也没关系,只要记住以下用法即可
//数字型变量转字符串
to_string();//c++全局函数
//字符串转数字
stoi();//to int
stol();//to long
stof();//to float
//都需要导入#include <string>
四舍五入,可以先double +0.5然后转int取整数部分,也可以用cmath的函数round()
数组,字符串或其它常用stl容器大规模清零或者填充数据可以使用fill()函数
// fill algorithm example
#include <iostream> // std::cout
#include <algorithm> // std::fill
#include <vector> // std::vector
int main () {
std::vector<int> myvector (8); // myvector: 0 0 0 0 0 0 0 0
std::fill (myvector.begin(),myvector.begin()+4,5); // myvector: 5 5 5 5 0 0 0 0
std::fill (myvector.begin()+3,myvector.end()-2,8); // myvector: 5 5 5 8 8 8 0 0
std::cout << "myvector contains:";
for (std::vector<int>::iterator it=myvector.begin(); it!=myvector.end(); ++it)
std::cout << ' ' << *it;
std::cout << '
';
return 0;
}
output
myvector contains: 5 5 5 8 8 8 0 0
将十进制a转换为b进制数,当a不为0时,将a%b从后往前倒序保存下来,每次保存后将a/b。这样倒序保存的数就是十进制a在b进制下的结果。
进制互转代码参考如下
#include<iostream>
#include<cstdlib>
using namespace std;
int main(){
//把8进制的17转化为10进制打印输出
string str = "17";
char *tmp ;
long result = strtol(str.c_str(),&tmp,8);
cout<<result;
return 0;
}
#include<iostream>
#include<algorithm>
using namespace std;
//digital为10进制数,r为需要转换的目标进制,返回目标进制数
string dtox(int digital,int r){
string result="";
const char s[37]="0123456789abcdefghijklmnopqrstuvwxyz";
if(digital==0){
return "0";
}
while(digital!=0){
int tmp =digital%r;
result+=s[tmp];
digital/=r;
}
reverse(result.begin(),result.end());
return result;
}
int main(){
cout<<"十进制10转为16进制结果:"<<dtox(10,16)<<endl;
cout<<"十进制10转为8进制结果:"<<dtox(10,8)<<endl;
cout<<"十进制10转为2进制结果:"<<dtox(10,2)<<endl;
cout<<"十进制10转为10进制结果:"<<dtox(10,10)<<endl;
}
尽量使用c++的string类
读取整行的代码如下
string str;
getline(cin,str);//该函数在std标准库中,不需要引入string头文件
c++的string类可以转化为c的字符数组,str.c_str();
int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
int lcm(int a,int b){
return a*b/gcd(a,b);
}
对于一些可以事先进行预处理然后用散列表来求解的问题,可以大大减少时间复杂度。比如一个需要大量查询斐波那契数列的问题中,我们可以事先把前N个斐波那契数列求解出来然后放到散列表中进行保存,之后的查询就都是O(1)的时间复杂度。
▲多利用位运算来求解交集,并集,差集,可以大大减少时间复杂度,降低编码难度。
素数的判断
bool isPrime(int n){
if(n <= 1) return false;
int sqr = (int)sqrt(1.0*n);
for(int i = 2;i<=sqr; i++){
if(n%i==0) return false;
}
return true;
}
常用C++ STL容器
C++ container
- Sequence containers
- Sequence container adapters
- Associative containers
- Unordered associative containers
- unique key
- same key
algorithm头文件常用函数
algorithm
- max
- min
- abs
- swap
- reverse
- is_permutation
- next_permutation
- prev_permutation
- fill
- sort
- lower_bound
- upper_bound
大数组必须定义为全局变量
字符数组要多开一个单位
string.find()返回的是下标的值,没有找到用==string::npos
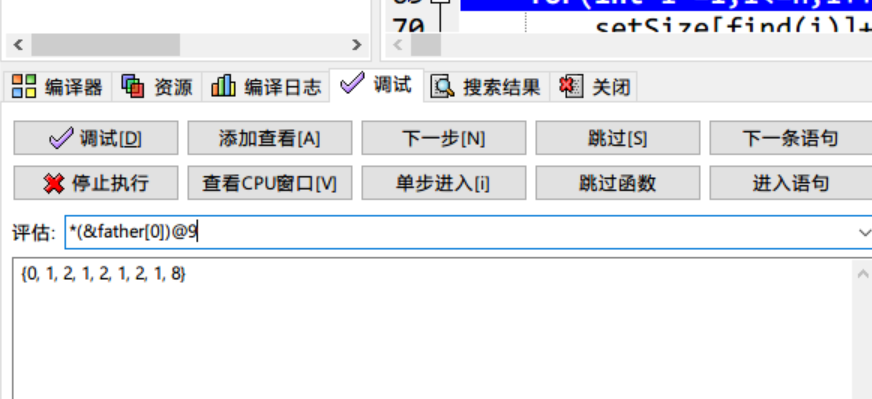
dev c++调试代码时,查看vector容器的内容
同时存在边权和点权的最短路径问题,求最短路径条数以及最大点权和、打印最短路径?
- 用一遍Dijkstra算法即可
- dis[i]表示从出发点到i结点最短路径的路径长度
- num[i]表示从出发点到i结点最短路径的条数
- w[i]表示从出发点到i结点点权的数目之和
- path[i]表示从出发点到i结点的前驱结点,利用栈(或者递归)打印路径即可
图的初始化
-
如果是无向图,需要注意初始化边的时候,是有两条边的,不能漏掉了
-
没有边的情况(包括两种情况,1.顶点v,w之间不存在边,2.顶点v本身没有到达自己的边),初始化为0,如果是初始化为-1,则判断边是否存在的时候需要注意G[i][j]<0而不是直接if(G[i][j]),这两种判断一个是判断0,一个是判断<0
-
图的初始化,可以用fill函数,具体用法可以参考如下
//必须添加algorithm头文件 #include<algorithm> //在内存地址区间[first,last)范围内,填充x fill(first,last,x); //但是特别注意二维数组的填充 int arr[2][2]; fill(arr[0],arr[0]+4,0); /* 这里需要注意的是,arr[0]表示的才是整个二维数组的起始地址,而不是arr,另外,这个区间是左闭右开区间!!! */不仅是图的初始化, 其它的辅助数组也可以用fill函数初始化,比如说path数组(用于记录顶点w的前驱顶点,打印最短路径),dist数组(用于记录出发点到顶点w的最短路径),num数组(用于记录从出发点到顶点w的最短路径条数),w数组(用于记录从出发点到顶点w的点权之和)等。
-
在真正进行Dijkstra算法之前,先检查下面这些数据是否都已经初始化好了
1.初始化图 2.初始化路径 3.初始化距离 4.初始化收录情况 5.初始化点 6.初始化出发点,以及出发点的邻接点的路径和距离信息
最短路径扩展问题
-
要求数最短路径有多少条
- count[s] = 1;
- 如果找到更短路:count[W]=count[V];
- 如果找到等长路:count[W]+=count[V];
-
要求边数最少的最短路
- count[s] = 0;
- 如果找到更短路:count[W]=count[V]+1;
- 如果找到等长路:count[W]=count[V]+1;
-
存在点权
比如救火问题,多条最短路径,选择点权最大的那条
for(int i = 0; i < n; i++) { int u = -1, minn = inf; for(int j = 0; j < n; j++) { if(visit[j] == false && dis[j] < minn) { u = j; minn = dis[j]; } } if(u == -1) break; visit[u] = true; for(int v = 0; v < n; v++) { if(visit[v] == false && e[u][v] != inf) { if(dis[u] + e[u][v] < dis[v]) { dis[v] = dis[u] + e[u][v]; num[v] = num[u]; w[v] = w[u] + weight[v]; } else if(dis[u] + e[u][v] == dis[v]) { num[v] = num[v] + num[u]; if(w[u] + weight[v] > w[v]) w[v] = w[u] + weight[v]; } } } } -
边权不唯一
比如旅游规划问题,存在多条最短路径时,选择花费最少的
void Dijkstra( Vertex s ) { while (1) { V = 未收录顶点中dist最小者; if ( 这样的V不存在) break; collected[V] = true; for ( V 的每个邻接点W ) if ( collected[W] == false ) if ( dist[V]+E<V,W> < dist[W] ) { dist[W] = dist[V] + E<V,W> ; path[W] = V; cost[W] = cost[V] + C<V,W> ; } else if ( (dist[V]+E<V,W> == dist[W]) && (cost[V]+C<V,W> < cost[W]) ) { cost[W] = cost[V] + C<V,W> ; path[W] = V; } } }
algorithm常用函数补充
所有的range都是左闭右开区间
//判断range1是否为range2(长度length2>=length1)的子序列,可以完全相等
is_permutation(first1,last1,first2);
//查找range2在range1中的位置
search(first1,last1,first2,last2);
//交换a和b的值
swap(a,b);
//填充range
fill(first,last,value);
//reverse反转一个range
reverse(first,last);
//判断range是否有序【升序asc】
is_sorted(first,last);
//获取从那个位置开始无序
is_sorted_until(foo.begin(),foo.end());
//一个有序range插入新元素x的最小插入位置
lower_bound (v.begin(), v.end(), 20);
//一个有序range插入新元素x的最大插入位置
upper_bound (v.begin(), v.end(), 20);
//合并两个range到一个新容器中
std::merge (first,first+5,second,second+5,v.begin());
//获取min
std::min(1,2)
//获取max
std::max(1,2)
//获取min_element
std::cout << "The smallest element is " << *std::min_element(myints,myints+7) << '
';
//获取max_element
std::cout << "The largest element is " << *std::max_element(myints,myints+7) << '
';
//获取一个range的一个序列
int main () {
int myints[] = {1,2,3};
std::sort (myints,myints+3);
std::cout << "The 3! possible permutations with 3 elements:
";
do {
std::cout << myints[0] << ' ' << myints[1] << ' ' << myints[2] << '
';
} while ( std::next_permutation(myints,myints+3) );//对应的就是更大的序列
std::cout << "After loop: " << myints[0] << ' ' << myints[1] << ' ' << myints[2] << ' ';
return 0;
}
输出结果
The 3! possible permutations with 3 elements:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
After loop: 1 2 3
类似的还有
std::prev_permutation(myints,myints+3) 返回一个bool
true if the function could rearrange the object as a lexicographicaly smaller permutation(字典序更小的子序列).
Otherwise, the function returns false to indicate that the arrangement is not less than the previous, but the largest possible (sorted in descending order).
开考前,可以先用记事本把一些常用的头文件写下来
注意求平均值的时候是否需要四舍五入,如果需要+0.5即可
排名问题,如果两个人分数一样,那么排名也是一样的,比如
第一种情况:
1,1,1,4,5,6
stu[0].rank[flag] = 1;
for(int i = 1; i < n; i++) {
stu[i].rank[flag] = i + 1;
if(stu[i].score[flag] == stu[i-1].score[flag])
stu[i].rank[flag] = stu[i-1].rank[flag];
}
第二种情况:
1,2,3,4,5
这种比较简单,可以直接使用for循环,或者while循环,临时变量每次自增1即可
通常都是第一种情况,如果是第二种情况的话,很可能会附加排序字段
fill函数对于重置exist,flag,visit等类型的数组很方便,也省时间,一般只在fill函数无法满足要求时才考虑使用遍历重置数组
求图的连通分量的个数
void dfs(int node) {
visit[node] = true;
for(int i = 1; i <= n; i++) {
if(visit[i] == false && v[node][i] == 1)
dfs(i);
}
}
int cnt = 0;
for(int j = 1; j <= n; j++) {
if(visit[j] == false) {
dfs(j);
cnt++;
}
}
还可以用并查集来求连通分量
中序和后序转先序
#include <cstdio>
using namespace std;
int post[] = {3, 4, 2, 6, 5, 1};
int in[] = {3, 2, 4, 1, 6, 5};
void pre(int root, int start, int end) {
if(start > end) return ;
int i = start;
while(i < end && in[i] != post[root]) i++;
printf("%d ", post[root]);
pre(root - 1 - end + i, start, i - 1);
pre(root - 1, i + 1, end);
}
int main() {
pre(5, 0, 5);
return 0;
}
循环输入
#include<iostream>
using namespace std;
int main(){
//cin循环输入测试
int a;
//只要输入的整数a不等于9,循环就会一直执行,直到输入9
while(cin>>a,a!=9){
printf("%d
",a);
}
return 0;
}
如果要在遇到换行符时退出循环,可以使用getchar()函数来判断
#include<iostream>
using namespace std;
int main() {
//cin循环输入测试
string tkey;
while(cin >> tkey) {
cout<<tkey<<endl;
char c = getchar();
if(c == '
') break;
}
return 0;
}