Java排序算法——堆排序

堆排序：
堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。

首先先来看一下什么是堆？
堆是具有以下性质的完全二叉树：
每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；
每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子：

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：
大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

堆排序基本思想：
将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列。

基本步骤：
a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

下面来看详细的步骤：

1.构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。
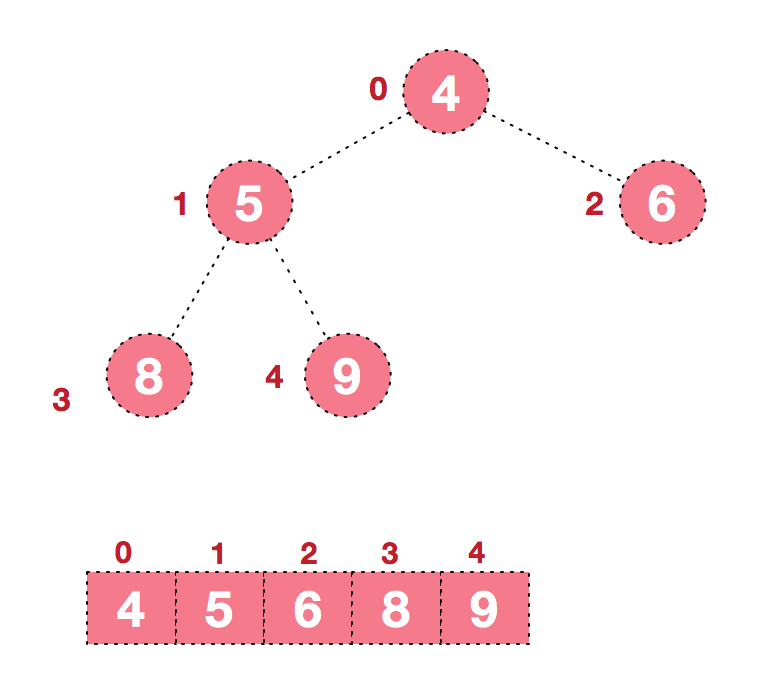
1.1 假设给定无序序列结构如下：

1.2 从最后一个非叶子结点开始，从左至右，从下至上进行调整，arr.length/2-1=5/2-1=1，也就是下面的6结点，由于[5,6,9]中9最大，这里就是6和9进行交换。

1.3 找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

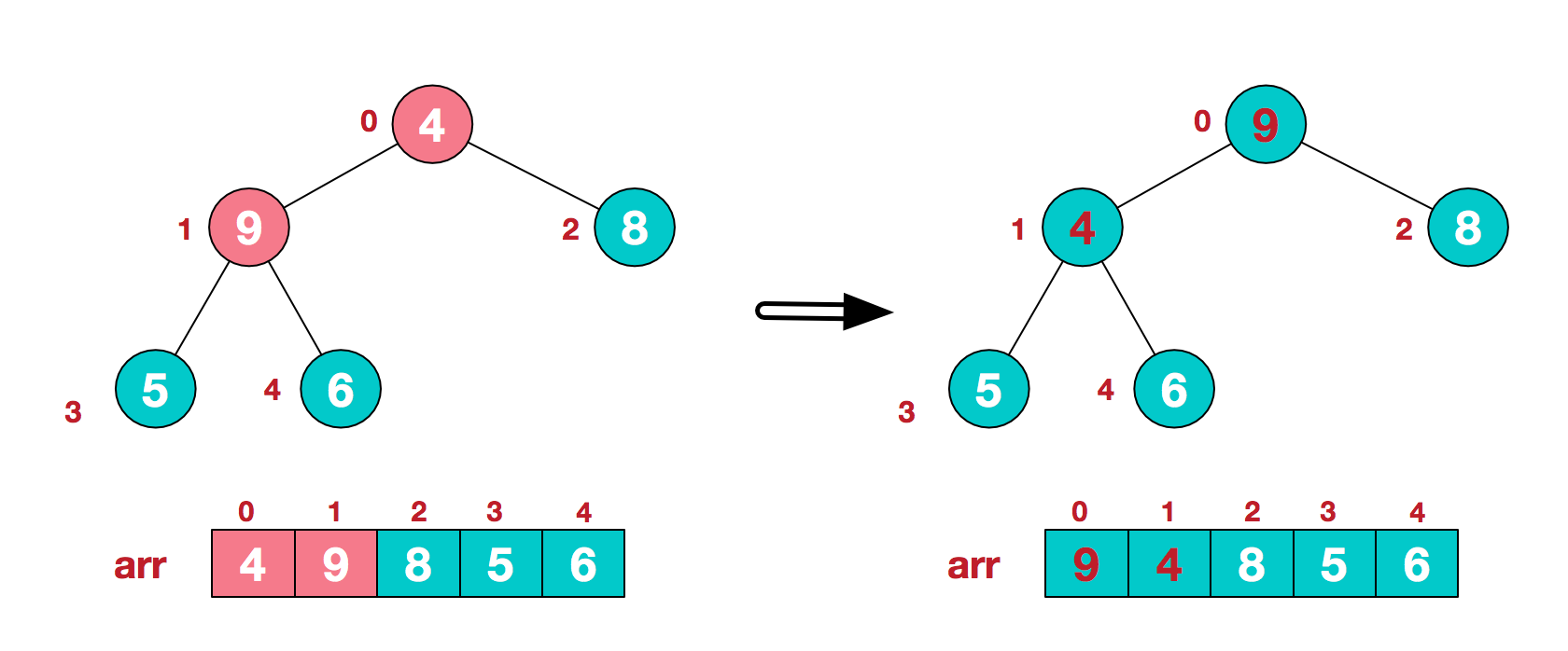
1.4 这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

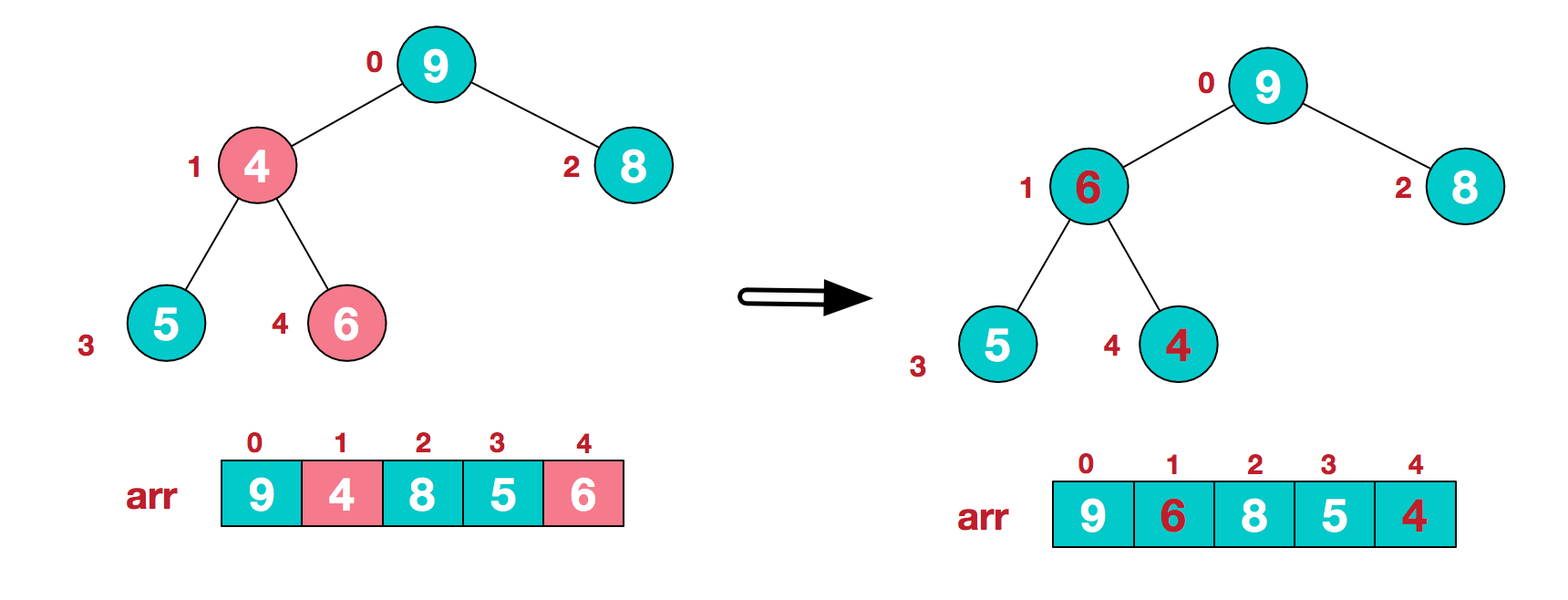
这样我们就将一个无需序列构造成了一个大顶堆。

2.将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。
2.1 将堆顶元素9和末尾元素4进行交换。

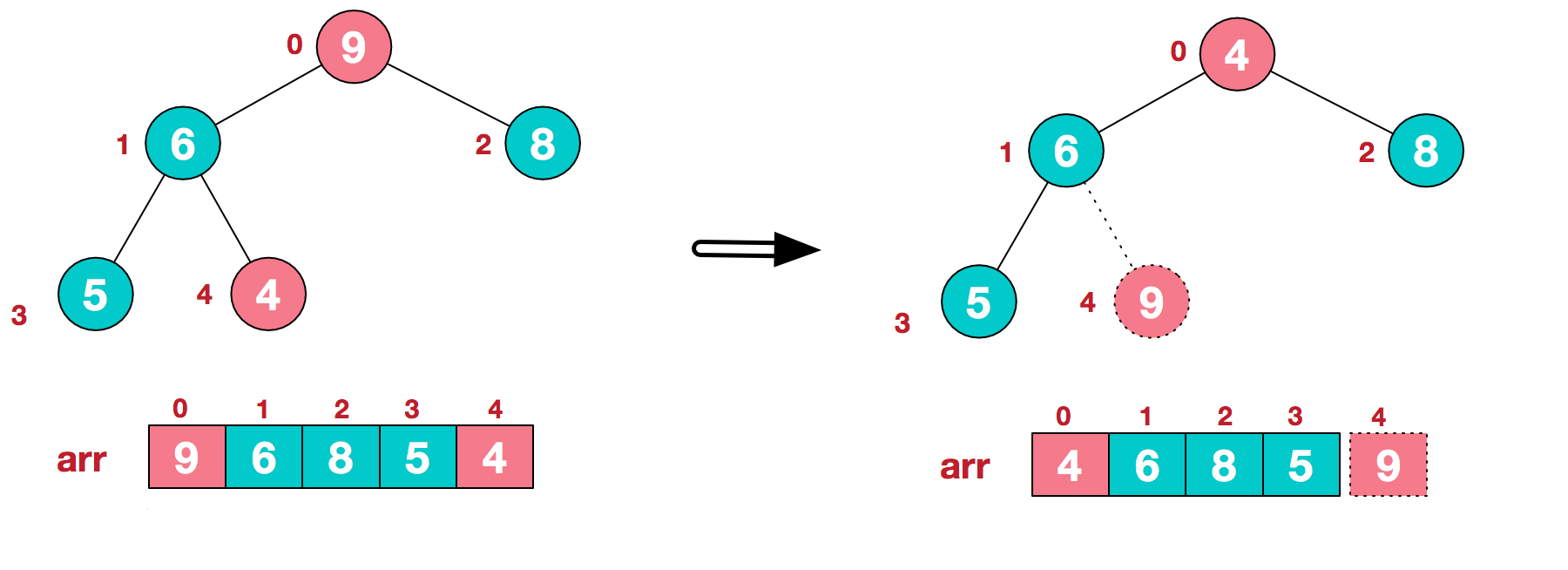
2.2 重新调整结构，使其继续满足堆定义。

2.3 再将堆顶元素8与末尾元素5进行交换，得到第二大元素8。

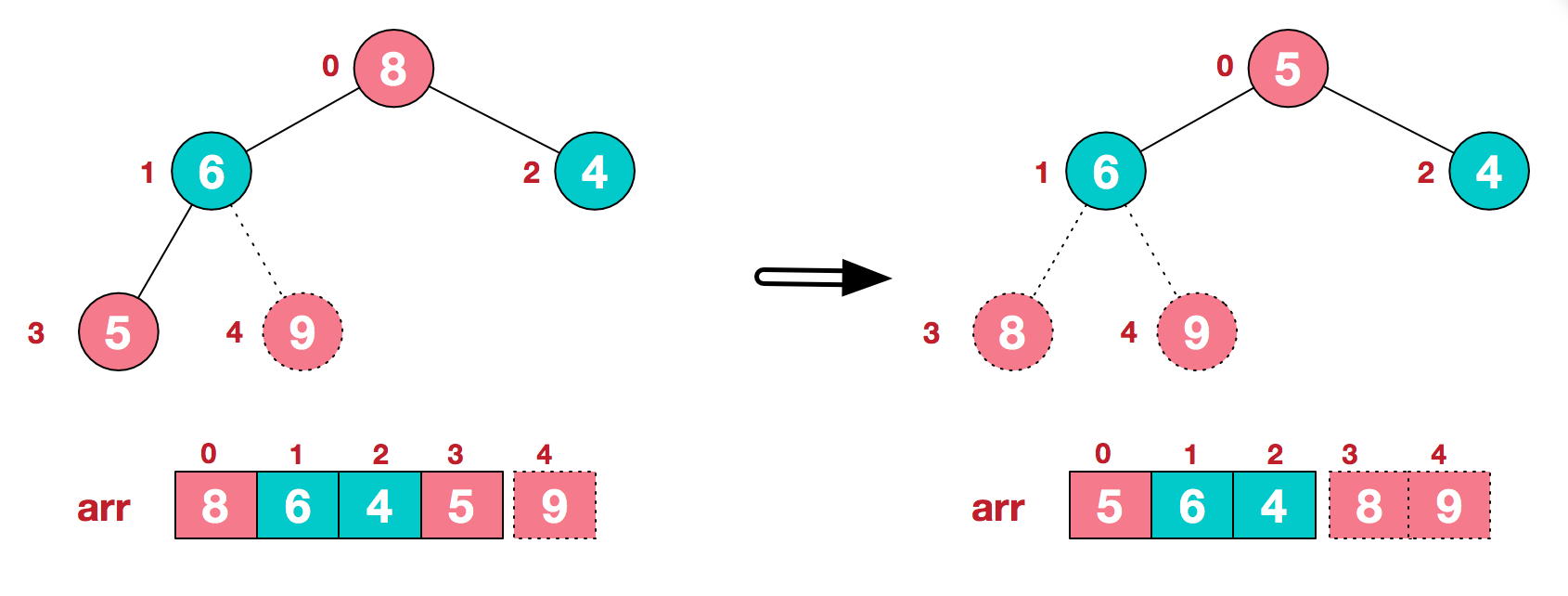
3.后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序。

下面是java代码实现：

import java.util.Arrays;

public class HeapSort {
public static void main(String[] args) {
int arr[] = { 4, 6, 8, 5, 9 };
heapSort(arr);
System.out.println(Arrays.toString(arr));
}

private static void heapSort(int[] arr) {
// 构建大顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
// 从第一非叶子结点开始调整
changeHeap(arr, i, arr.length);
}
// 调整堆结构和交换堆顶元素与末尾元素
for (int j = arr.length - 1; j > 0; j--) {
swap(arr, 0, j);// 将堆顶元素与末尾元素进行交换
changeHeap(arr, 0, j);// 重新对堆进行调整
}
}

/*
* 交换元素
*/
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}

/*
* 调整大顶堆
*/
private static void changeHeap(int[] arr, int i, int length) {
int temp = arr[i]; // temp暂存当前元素
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {// 从i结点的左子结点开始，也就是2i+1处开始
if (k + 1 < length && arr[k] < arr[k + 1]) {// 如果左子结点小于右子结点，k指向右子结点
k++;
}
if (arr[k] > temp) {// 如果子节点大于父节点，将子节点值赋给父节点
arr[i] = arr[k];
i = k;
} else {
break;
}
}
arr[i] = temp;// 将temp值放到最终的位置

}
}