OpenCASCADE Rolling Ball
在《The NURBS Book》书中引入了三边球面片(Three-sided Spherical Surface)的概念:
当三个曲面两两相交时,会使三边界曲线交于一个角点(如图a),由于在产品零部件中,尖边和尖角经常是我们不希望有的,一方面是会有应力集中,另一方面尖的部分容易使人受伤。因此,经常需要对曲面的尖边和尖角进行处理,使其变得光滑,这种操作通常称为“圆角”或“倒角”,所得到的曲面称为圆角曲面(Fillet Surface)。一个常用的获得圆角曲面的概念性方法是“滚球法”(Rolling marble)。设一个半径为R的小球在物体内侧沿着所有的边界曲线滚动,得到图b中所示的曲面S4-S7, S4-S6为倒边曲面(edge fillet),S7为倒角曲面(Corner fillet)。倒角曲面S7是一个三边曲面片(Three-side patch)。

在实际造型时也经常需要对曲面连接部分进行光滑处理,除了常见的倒角Chamfer和倒圆Fillet以外,opencascade也提供了rolling ball的造型算法用来对相边曲面进行圆滑处理,如下图所示: 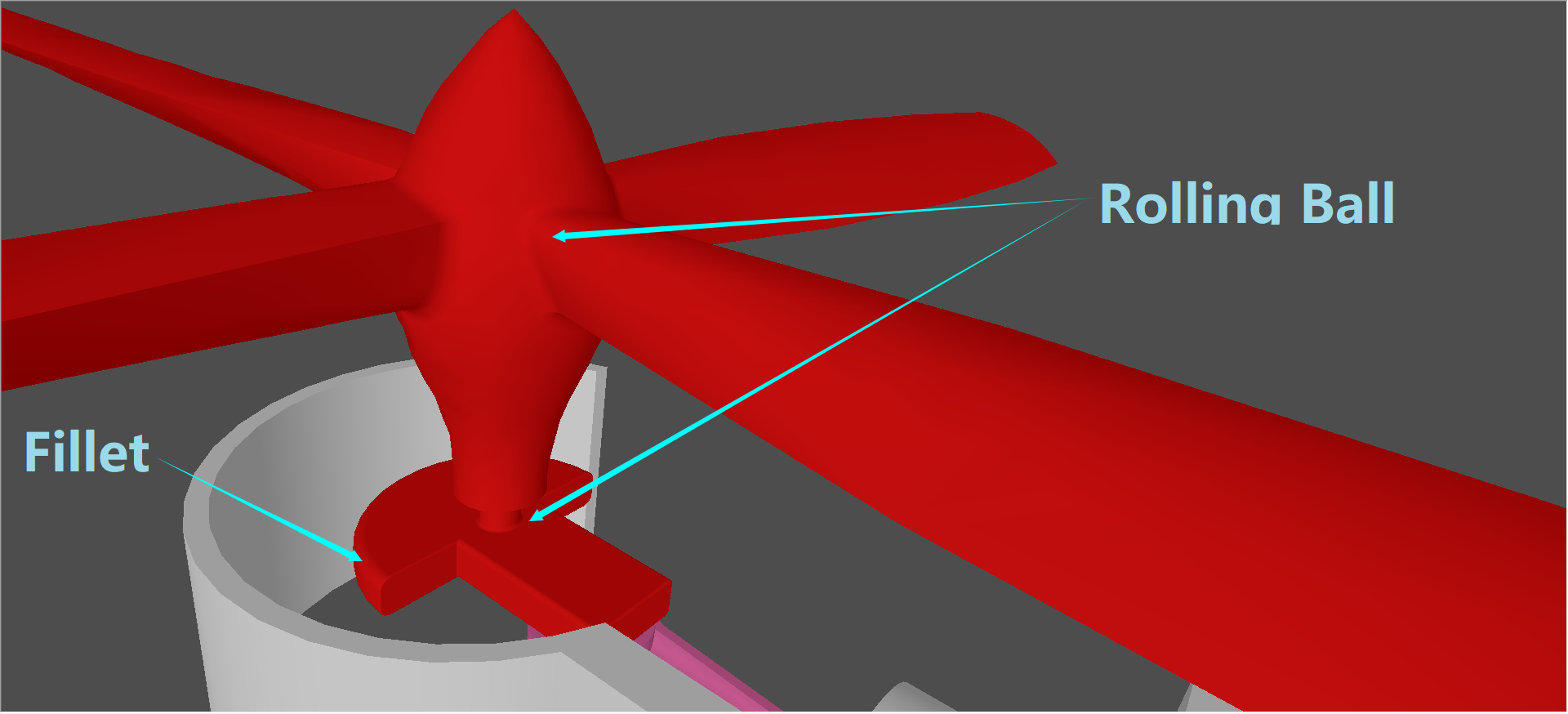
如下图所示为对圆柱相连部分使用“Rolling Ball”生成一个圆滑过渡的圆弧曲面。
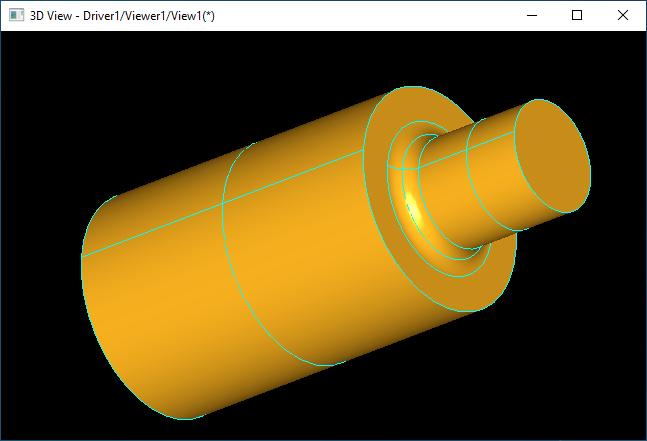
对于这种对称的模型,也可以使用旋转造型算法,把轴的外轮廓构造出来,再绕轴线旋转一周也可以得到。当相连曲面部分不对称的时候,旋转造型也无能为力了。
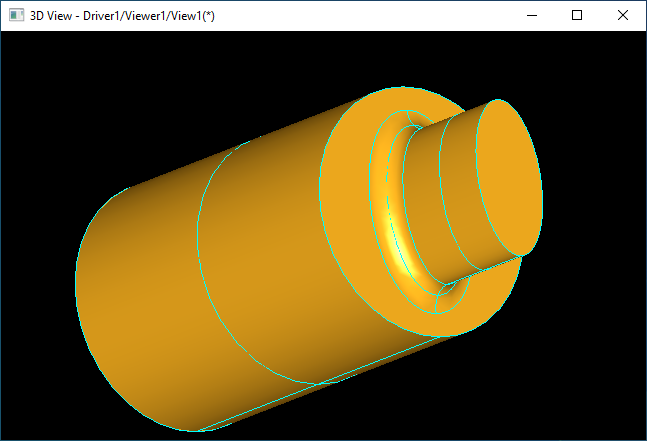
如上图所示,当相连接部分是不对称的曲线椭圆时,旋转造型算法已经不适用,这时就需要使用“滚球法”来对连接部分进行处理。对于更复杂的情况,如下图所示的也适用。
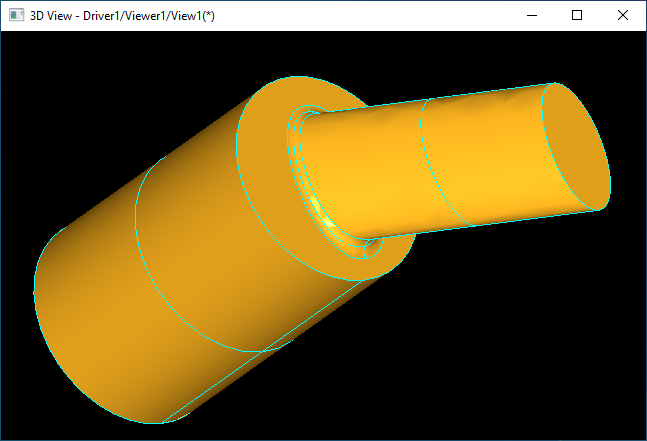
这里先引入opencascade中对相连曲面圆滑处理的造型算法“滚球法”Rolling Ball,有兴趣的同学可以自己尝试。对实现原理感兴趣的,可以自己Debug源码。希望有更多人去深究源码,做到知其所以然,提高数学的应用水平。
