卡特兰数#
部分资料来源于
https://www.bilibili.com/video/av96018454
https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746?fr=aladdin
引入##
有m+n个人站成一排要进入剧院,门票是50元。其中有n个人有整50元,而m个人只有一张整100元。售票处一开始没有零钱,这些人需要以某种方式排队,使得售票处总有零钱可找,求可行方案数。
基本模型##
给定n个0,m个1
问有多少序列,满足:
(1)n个0,m个1完全被使用
(2)对于任意前k个数,1的个数不少于0
理论##
我们应该将问题转换成如下的东西处理:
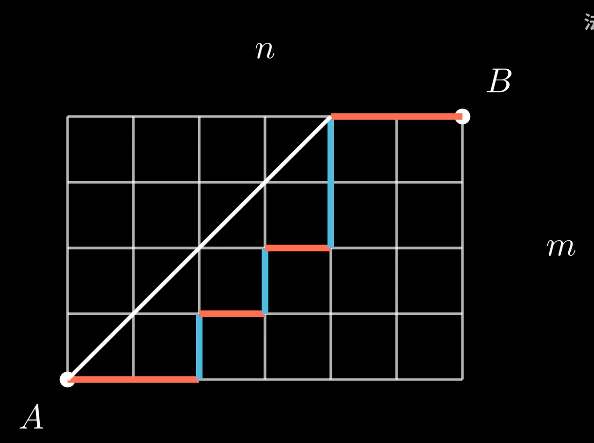

如图,从左下出发到右上结束,选择一条只能向上或向右的路径。
那么这样约束条件(1)中0和1数量就转换成了图中的横竖边数
而约束条件(2)的实现,无非就是路径选择上不能越过如图白色斜线
处理问题的方法##
(1)DP###
数据规模比较小的情况下,可以采用DP的思想,降空间复杂度可以掏个滚动数组。
(2)折线法###
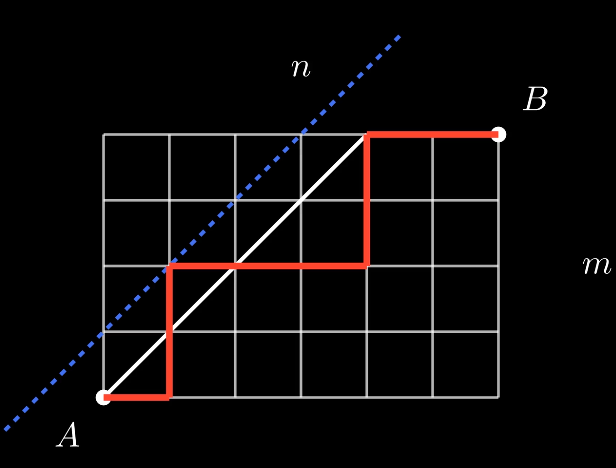
显然如图,只要与蓝线有交点的线,它就是不满足条件的线。
那么我们去研究符合条件的路径无非就是用总的路径数减去不符合条件的路径
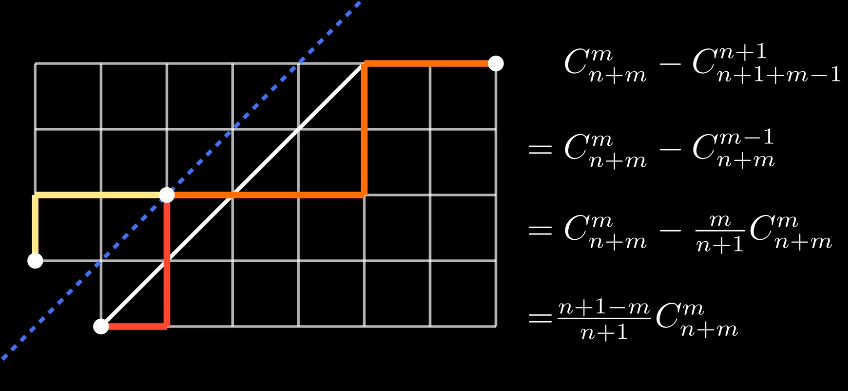
我们把某条不合法路径A->C->B与蓝线的首个交点记为C。我们把左下角为A、右上角为蓝线末端的矩形以蓝线为对称轴对称过去,那么我们就可以得到宽为(m-1)长为(n+1)的一个矩形

把所有非法路径与蓝线首次相交的点一下镜像对称过去,如A->C->B也就成了A'->C->B,显然它穿过蓝线。
我们先看一下新矩阵,任意一条从A'->B的路径,它一定会穿过蓝线,也就是说,新矩形上选取的任意路径对应的原镜像路径都是非法的。
而又由于非法路径上的非法交点一定是在我们镜像的矩阵内,并且只要路径与蓝线有交点(无论多少个),它的起点到它的首个非法点之间就能形成镜像路径,并且与它后面的路径能够"无缝"衔接这条镜像路径,所以说明原图上所有非法路径均能在新矩阵上形成一条非重叠的新路径。
由此,我们可得,原图非法路径与新图非法路径是一一匹配的。
那么非法路径的数量也就引刃而解了。
推广##

详见:https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746?fr=aladdin
模式变形##
卡特兰数真是一个神奇的数字,很多组合问题的数量都和它有关系
Q:出栈序列问题:一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
(转换为01串处理即可)
Q:给顶节点组成二叉树的问题:给定2n+1个节点,能构成多少种不同的二叉树?
A:显然叶节点数量为n+1个,非叶节点为n个,即非叶节点为0,叶节点为1,考虑先序遍历形成的01字符串,这个先序遍历的字符串尾部一定是1,不影响构造数,要忽略。那么对于剩下的2n个数,因为是先序遍历,所以非叶节点的数量一定比叶节点多,其必然满足卡特兰数的形成条件。
Q:括号化连乘问题:P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对二元的乘积(括起来的看作一元),试问有几种括号化的方案?
(等价于:对于n+1个元相乘,试问有多少添加括号的方式,使得元素位置不变、
乘法运算顺序改变)
A:对于这类问题,可以看成上面一种的演变,即把每个元看成上面二叉树的叶节点(中序遍历叶的顺序就是各元在序列中的位置),每次相乘看成一个节点,而根的深度越大,就表明两者乘积的优先度越高,这样一来我们就把问题处理成上面的问题了。
Q:n对括号正确匹配数目:给定n,问有多少种正确匹配的排列方式
(转换成01串处理即可)
Q:凸多边形划分三角形问题:在一个凸多边形中,通过若干条互不相交的对角线,把这个多边形划分成了若干个三角形。任务是键盘上输入凸多边形的边数n,求不同划分的方案数f(n)。
结论:对凸n+2边形进行不同的三角形分割(只连接顶点对形成n个三角形)数为Cn
比如当n=6时,f(6)=14。
A:无论怎么划分,对于一条确定的边而言,它肯定属于一个三角型,那么我们研究h(n)的时候,无非就固定一条边,去枚举点的情况即可,这样构造的三角形会将原凸多边形,分割成两个小的凸多边形,那么根据乘法原理,将两个凸多边形的子结果相乘,即可得到卡特兰数的递推形式。
很多时候,就像做博弈论的题目一样,你不打个表,手写个枚举,很难发现规律,所以,在做题的时候,合适地列出前几项来。
P1641 [SCOI2010]生成字符串 逆元+卡特兰数##
AC代码:
#include<iostream>
#include<cstring>
using namespace std;
#define INF 1e10+5
#define maxn 105
#define minn -105
#define ld long double;
#define uint unsigned int;
#define ull unsigned long long;
typedef long long ll;
const ll mo=20100403;
ll min(ll a,ll b)
{
return a<b?a:b;
}
ll faspow(ll a,ll pow)
{
ll ans=1;
while(pow)
{
if(pow&1)ans*=a,ans%=mo;
a=a*a%mo;
pow>>=1;
}
return ans;
}
ll inver(ll a)
{
if(a==1)return 1;
return faspow(a,mo-2)%mo;
}
ll cal(ll n,ll m)
{
ll ans=1;
for(int i=1;i<=m;i++)
ans=ans*(n+1-i)%mo*inver(i)%mo;
return ans;
}
int main()
{
cin.tie(0);
cout.tie(0);
ios_base::sync_with_stdio(false);
ll n,m;
cin>>n>>m;
if(n<m)
{
cout<<0<<endl;
return 0;
}
ll ans=0;
ans=cal(n+m,m)%mo-cal(m+n,m-1)%mo+mo;
cout<<ans%mo<<endl;
return 0;
}