(Day1 - Day7)
(CF643G)
考虑 (50\%)的情况 , 每次取出两个不相同的数将它们删除 , 那么最后得到的必然是绝对众数。
这个做法显然可以扩展到任意比例的情况 , 只需要将操作改成 "取出 (K) 个并删除" 即可。
可以用线段树维护。
时间复杂度 : (O(C(N + Q)logN)) 取 (C = 100)。
(CF1083D)
对于区间 ([b , c)) , 记 (pre_{i}) 表示 (a_{i}) 出现在左边第一个的位置 , (suf_{i}) 表示 (a_{i}) 出现在右边第一个的位置。
那么其贡献就是 ((b - max{pre})(min{nxt} - c))。
枚举右端点 (c) , 单调栈 + 线段树维护即可。
时间复杂度 : (O(NlogN))
(CF1172F)

观察 (sum) 函数 , 发现其输出必然是输入值减去了若干个 (p)。
考虑一个 (O(N sqrt{NlogN})) 的做法 , 首先将序列分块 , 定义函数 (F(i , x)) 表示权值为 (x) , 输入到第 (i) 个块中 , 最后的输
出值是多少 , 这个函数可以在 (O(B ^ 2)) 的时间内预处理出。 回答询问只需在块内查询即可。
考虑优化这个做法 , 首先观察发现 , (x - F(x)) 这个函数是单调不降的 , 也就是说 , ((x + 1)) 一定比 (x) 减去的值更多。
接着 , 可以通过归纳法证明 , (x - F(x)) 这个分段函数至多是 ((l + 1)) 段。
因此 , 建出线段树 , 对于线段树上每个区间求出分段函数 , 合并两个分段函数的时候用 (two - pointers) 扫描。
查询时 , 只需在线段树分成的 (O(logN)) 个区间内二分即可。
时间复杂度 : (O(Qlog^2N))。
(CF896E)
首先将序列分块。 用链表 (f_{i , x}) 表示第 (i) 块中权值为 (x) 的数字集合。
对于操作 , 如果值域比 (2x) 大 , 就将 ([1..x]) 内的数向上合并 , 否则将 ([x + 1..max]) 向下合并。
对于询问 , 直接求链表长度即可 , 可以通过并查集维护。
定义一个区间的势能为其极差 , 不难发现这样的做法在 (O(x)) 的时间内使得一个块的势能减小了 (x)。
故时间复杂度 : (O((N + Q)sqrt{N})) (值域与 (N) 同阶)
(CF1083F)
首先考虑最朴素的做法 : 从小到大枚举 , 遇到不同的就翻转。
定义差分序列 (c_{i} = a_{i} oplus b_{i} oplus a_{i - 1} oplus b_{i - 1}) , 那么每次操作只修改了 (c_{i}) 的两个位置。
因为每次影响到的两个数在模 (K) 意义下相同 , 故可以将序列按下标值模 (K) 分组。
对于一组而言 , 其答案为前缀异或和非零的数的个数 , 其理由在于 : 一个前缀异或值为 (0) 的数必然将答案减小了 (1)。
考虑根号分治。 当 (k geq sqrt{N}) 时 , 每次直接暴力修改 , 否则 , 将序列分为若干块 , 对每块打上整体标记并维护块内每个数的出现次
数即可。
时间复杂度 : (O((N + Q)sqrt{N}))。
(LOJ 3366)
来源于国际信息学竞赛 (2020)。
首先一个显然的结论是 , 游戏负责人必然会选择玩家抽到数字中的中位数 , 因为这会使其收益最小化。
因此 , 这等价于每次选出的 (K) 个数中 , 有 (frac{N}{2}) 个贡献为 (1) , 而其余的贡献均为 (-1)。 最大化贡献之和。
继续将这个问题进行转化 , 其等价于 : 每行选出 (K) 个数 , 在所有选出的 (NK) 个数中选择一半贡献为正 , 另一半贡献为负。 求出最大的总和。
可以用调整法证明只要找到一组解这组解就合法。
那么这个问题就很容易了 , 只需用一个堆每次贪心取贡献最大的二元组就可以了。
时间复杂度 : (O(NKlogK))。
(LOJ3365)
来源于国际信息学竞赛 (2020)。
首先如果存在 (p_{i , j} geq 3) , 那么必然无解。 因为这样必然存在两点满足其不同的路径数超过 (3) 条。
对于 (p_{i , j} = 0) 的情况 , 相当于将这张图分割成若干联通分量。
对于剩下的点集 , 用链 + 环构造即可。 需要用并查集维护。
时间复杂度 : (O(Nalpha(N)))
(Day 8 - Day14)
(CF1396E)
首先 , 对于每一条边 , 记其贡献为 (c_{e})。 设这条边将树分成两部分大小分别为 (x_{e}) 和 (y_{e}) , 令 (z_{e} = min(x_{e} , y_{e}))。 则 :
(1) : 至少有 (z_{e} mod 2) 个点经过 (e)。
(2) : 至多有 (z_{e}) 个点经过 (e)。
综上 , 有 (z_{e} mod 2 leq c_{e} leq z_{e}) , 因此得到 : (sum_{e}{(z_{e} mod 2)} leq S(f) leq sum_{e}{z_{e}})。
而 (S(f) = frac{1}{2} sum_{i}{depth_{i} + depth_{f_{i}} - 2 cdot depth_{lca(i , f_{i})}})。 与 (sum_{e}{z_{e}}) 模 (2) 意义下同余。
至此 , 得到了有解的一个必要条件。 也就是 (sum_{e}{(z_{e} mod 2)} leq S(f) leq sum_{e}{z_{e}}) 且 (S(f)) 与 (sum_{e}{z_{e}}) 模 (2) 同余。
接着考虑证明这个条件同样是充分的。
不妨记 (L(T) = sum_{e}{(z_{e} mod 2)}) , (R(T) = sum_{e}{z_{e}}) 并取树的重心 (G) 为根建树。
约定 (size(u)) 表示以 (u) 为根的子树大小 , (depth(u)) 表示 (u) 节点的深度。
考虑数学归纳法 :
当 (N = 2) 时 , 树的形态只有 (1) 种 , 显然成立。
若 (N = 2M - 2) 时成立 , 考虑 (N = 2M) 的情况 :
当 (K = R(T)) 时 , 由树重心的性质 , 直接将 (DFS) 序上 (i) 号节点向 (i + frac{N}{2}) 节点连边即可。
否则 , 取 (G) 的儿子节点 (g) , 使得 (size(g)) 最大。 取节点 (w) 为 (g) 中深度最大且 (size(w) leq 2) 的节点。
若 (K + 2 cdot depth(u) leq R(T)) , 若 (w) 有 (2) 个儿子 , 直接将这两个儿子匹配 , 否则将 (w) 和其仅有的儿子节点匹配。 不难发现问题转化为 (N = 2M - 2) 且 (L'(T) leq K' leq R'(T)) 的情况。并且由树重心的性质 , 删去这两个点后树的重心仍然是 (G)。 继续递归构造即可。
否则 , 子树 (g) 中必然存在一点使得 (K + 2 cdot depth(u) = R(T))。 找到这个点并与其任意一个儿子节点匹配。 问题就转化为了 (K = R(T)) 时的情况。
用平衡树维护这个过程 , 时间复杂度 : (O(NlogN))。
(CF1422F)
首先讲讲我的做法 :
考虑若干个数的最小公倍数 , 本质是对每个质因子指数取最大值。
发现值域并不大 , 因此可以分为不超过 (sqrt{val}) 和超过 (sqrt{val}) 分别考虑。对于超过 (sqrt{val}) 的质因子最多只有 (1) 个 , 可以用可持久化线段树维护。 而不超过 (sqrt{val}) 的质因子数量并不多。 因此只需维护约为 (frac{sqrt{val}}{log(val)}) 棵支持查询区间最值的线段树即可。 时间复杂度 : (O(?))。
事实上存在更加优秀的做法 : 不妨枚举质因子的次幂 , 记 (pre_{i}) 表示上次出现 (i) 这个数是在哪个位置 , 那么只需在当前位置去除上个位置的影响 , 并加入新的数的影响即可。 可以用 (1) 棵可持久化线段树维护。
时间复杂度 : (O(NlogN))
(CF1167F)
考虑 (a_{i}) 的贡献 , 为 ((n - i + 1) cdot sum_{j = 1}^{i - 1}{[a_{j} < a_{i}] cdot j} + i cdot sum_{j = i + 1}^{n}{[a_{j} < a_{i}] cdot (n - j + 1)})。
这是个二维偏序 , 可以用树状数组维护。 时间复杂度 : (O(NlogN))。
(CF1254D)
对于每个修改操作 , 令根节点为 (v)。 那么 (u) 被加 (d) 当且仅当 (u) 和 (r) 不在同一棵子树中 , 其概率为 (frac{n - size(u)}{n})。
考虑树上差分并用树状数组维护。 但每个点的儿子最多有 (O(N)) 个。
处理这样的情况有一个常用的方法 , 对树进行轻重链路径剖分 , 在修改时只修改重儿子 , 并维护轻儿子的信息。
时间复杂度 : (O(Nlog^2N))。
(CF1416D)
考虑离线 , 倒着处理修改操作 , 此时删除操作相当于加边并且构成树形结构。
建出这棵重构树。 并用 (DFS) 序 + 线段树维护子树最值即可。
时间复杂度 : (O(NlogN))。
(10) 月 (13) 日训练
现场得分 : (0 + 30 + 100 = 130)
(A)
容易发现矩阵的秩就是答案。时间复杂度 : (O(N ^ 3))
对精度的处理不当会导致得到 (0) 分的成绩。 (EPS) 最好设成 (10^{-3})。
(B)
首先用 (Pollard-Rho) 算法对 (val_{1}) 做质因数分解。 并通过其质因子求出其所有的因子 (不超过 (2 ^ {15})个)。
考虑一种朴素的动态规划做法 : 记 (f_{i}) 表示节点 (i) 的答案 ,将 (val_{1}) 的因子标号 , 并记 (g_{i}) 表示权值对应标号为 (i) 的节点的 (f)
值总和。 (f) 的值可以通过 (g) 来求出 , 而 (g) 的值可以在 (DFS) 时的时候顺带维护。 这个做法的复杂度是 (O(N cdot 2^M)) 的(取 (M = 15))。
注意到 (2 ^ {15}) 这个数非常特殊 , 且查询的复杂度远低于修改的复杂度 , 于是考虑平衡规划 , 记 (h_{i , j}) 表示上一次选择的数前 (7) 位为 (i) , 后 (8) 位为 (j) 的方案数。 那么复杂度就优化到了 (O(N cdot 2^{frac{M}{2}}))。
事实上在这题中质因数分解并不需要用 (Pollard - Rho) 算法。 只需先找出 (10 ^ 7) 以内的质因子 , 去除这些质因子 , 将剩下的数和其他的数求最大公约数即可。 如果没有找到 , 那么无论剩下的数是否是质数都是无关紧要的。
(C)
考虑容斥原理。 答案为 :
(三个点的总贡献 - 至少有一条边的贡献 + 至少有两条边的贡献 - 三元环的贡献)。
其正确性在于 : 对于任意三个互相之间没有边的点 , 在这个式子中被计算了 (1) 次。
对于任意三个互相之间有一条边的点 , 在这个式子中被计算 (1 - 1 = 0) 次。
对于任意三个互相之间有两条边的点 , 在这个式子中被计算了 (1 - 2 + 1 = 0) 次。
对于一个三元环 , 被计算了 (1 - 3 + 3 - 1 = 0) 次。
故只有符合要求的情况被统计到答案中。
总贡献 , 至少一条边的贡献和两条边的贡献都是很好处理的。
而三元环的贡献可以通过这篇文章中的技巧做到 (O(N sqrt{N})) : 链接
时间复杂度 : (O(N sqrt{N})) , 需要注意细节的实现。
(10) 月 (14) 日训练
现场得分 : (100 + 60 + 40 = 200)。
(A)
记 (dp_{i}) 表示第 (i) 天为晴天的概率。
根据期望的线性性将每天的贡献求和即可。
(B)
首先考虑一个最简单的矩阵 , 将 (1) 到 (NM) 从大到小填入其中。
如何从这个最简单的矩阵推出收益最大的矩阵呢?
一种很优的贪心方式是 : 从最后一行最后一列开始依次扫描 , 将当前数尽可能变大。 这样可以做到 (O(M ^ 2))。
考虑加速这个过程 , 首先算出最多能将多少行加到满。 然后最多只需要对剩下的两行进行上述贪心即可。 时间复杂度 :(O(M))
(C)
考虑建出笛卡尔树。
对于一组询问 , 找出其 (LCA) , 答案即为 : 从 (LCA) 走到 (L) 向左走的次数 + 从 (LCA) 走到 (R) 向右走的次数 + 1。
离线 (Tarjan) / (ST) 表预处理 (LCA) 即可。
时间复杂度 : (O(MlogN))。
(CF1430D)
首先将 (0) 和 (1) 的连续段合并。
考虑删除数时让两个连续段合并必然不优 , 因此对于每个位置向后找到第一个大于 (1) 的段即可 , 可以用一个指针扫描。
时间复杂度 : (O(N))
(CF1430G)
考虑记 (dp_{S}) 表示剩余点集为 (S) 的答案。
枚举一个集合将它们标号 , 计算其贡献并转移即可。 要用高维前缀和预处理答案。
时间复杂度 : (O(3 ^ N))。
事实上这题还可以做到 (O(Poly(N))) , 对于每个点建 (N) 个对应权值的点 , 那么求最小割即可。
(CF1408G)
考虑一个点集合法的条件是形成了一个团。 否则一定是不行的。
因此只需建出 (Kruskal) 重构树 , 在树上做背包即可。
时间复杂度 : (O(N ^ 2))
(CF568C)
首先判断是否可行是个经典的 (2 - SAT) 问题。
考虑深度优先搜索构造方案 , 事实上在这题上搜索的复杂度只有 (O(N)) , 用一个 (std :: bitset) 维护不可行的点即可。
时间复杂度 : (O(frac{N ^ 3}{w})) (取 (w = 32))
(CF1381C)
首先考虑 (X = 0) 的情况。 即要求 (A) 中和 (B) 中有 (Y) 个元素相同 , 但必须错位排列。 当 (Y = N) 时 , 问题转化为广义错排问题。 即要求出现次数最多元素不超过 (frac{N}{2})。 而对于 (Y < N) 的情况 , 依然按照 (Y = N) 时的构造方式做一遍 , 设 (B) 与构造出的数组有相同元素的下标为 (K) , 并设 (f) 为 (B) 中出现次数最多的元素个数。
那么有 : (K = max(f - lfloor {frac{N}{2}} floor , 0))。
注意到一定有一个元素满足 (1 leq e leq N + 1) , 且该元素未在 (b) 序列中出现。 因此可以将这个数填充到 (k) 个相等的位置中。
因此当且仅当 (K leq N - Y) 时成立。
现在考虑 (X eq 0) 的情况。 有一个显然的贪心策略 : 每次取出现次数最多的并将其替换为 (e)。 那么用堆维护即可。
时间复杂度 : (O(NlogN))
(CF1387B1)
考虑一棵子树只会对其父节点贡献 (0 / 1) 个点。
那么直接构造就行了。
时间复杂度 : (O(NlogN))
(CF1387B2)
记 (x_{e} , y_{e}) 分别表示删去边 (e) 后的两个联通块大小。
考虑答案的上界 , 为 :
(sum_{e}{min{x_{e} , y_{e}} cdot 2w_{e}})
取树的重心 (G) , 那么根据重心的性质 , 其每个儿子节点的 (size) 值不超过 (lfloor frac{N}{2} floor)。故直接用广义错排问题中的构造方式构造即可。 这样答案可以取到上界。
事实上并不需要取树的重心 , 只需以任意节点为根就行了 , 因为假设两个在 (DFS) 序中距离为 (frac{N}{2}) 的节点在 (G) 对应的儿子的同一子树中 , 这个子树的大小就超过了 (frac{N}{2})。与重心的性质矛盾。
时间复杂度 : (O(N))。
(AGC018D)
如果重心在边上 , 答案为 (S - w)。
否则答案为 (S - min{e_{i}})。
正确性可以构造证明。
时间复杂度 : (O(N))
(CF571D)
首先将询问和操作离线。
根据前两种操作 , 可以建出两棵重构树 (T1 , T2)。
运用树状数组上二分 , 在 (T2) 上求出每个节点最后一次被清零是什么时候。
再在 (T1) 上求出询问的答案即可。
时间复杂度 :(O(QlogN))。
(CF582D)
考虑 (p ^ alpha | {n choose m}), 记 (v_{p}(n)) 表示 (n) 中 (p) 的指数是多少。
显然 , (v_{p}(n) = sum_{k}{lfloor frac{N}{p ^ k} floor})。
那么一对二元组 ((n , m)) 满足要求当且仅当 (v_{p}(n!) - v_{p}(m!) - v_{p}((n - m)!) geq alpha)。
下取整很难化简 , 但注意到 (lfloor frac{n}{p ^ k} floor = frac{n - n mod p ^ k}{p ^ k})。
于是得到 :
(原式 = frac{m mod p ^ k + (n - m) mod p ^ k - n mod p^k}{p ^ k})
观察后发现如果 (p) 进制下 ((n - m)) 产生一个进位 , 则 (p) 因子数多了 (1)。
于是问题转化为了一个经典的数位动态规划模型。
时间复杂度 : (O(N ^ 2))
(CF582E)
首先建出表达式树 , 表达式树的好处在于可以通过子树信息合并得出根结点的信息。
记 (f_{i , S}) 表示根结点为 (i) , 带入等式后得到的式子为 (S) 的方案数。
转移可以用 (FWT) 合并。
时间复杂度 : (O(N2 ^ N))
正睿十连测第六测 :
(A)
双指针即可。
时间复杂度 : (O(N))。
(B)
首先将正数和负数分开做。
考虑全是正数的情况 , 维护一个堆 , 初始时将二元组 ((1 , 0)) 放入堆中 , 每次取出堆顶 , 将 ((s + a_{i + 1} , i + 1) , (s - a_{i} + a_{i + 1} , i + 1)) 加入堆中。 这样的空间复杂度是 (O(KlogK)) 的。
做完这部分后 , 对每个正数维护一个负数指针 , 再用一个堆维护即可。
时间复杂度 : (O((N + K)logK))
(C)
记有 (w) 行有车 , (h) 列有车 , 那么一个答案即为 (mw + hn - wh)。
因此要求的就是 ([l1 , r1]) 中有多少个 (i) 满足有一个 (i) 第二维出现在了区间 ([l2 , r2]) 中。
对第一维莫队 , 第二维分块即可。
时间复杂度 : (O(N sqrt{N}log(N)))
正睿十连测第五测 :
(A)
首先 (K = 0) 的情况就是判定是否每个点的度数都为偶数。
考虑一个图求线图后 , 每条边在新图中的度数是 (deg_{u} + deg_{v} - 2)。
若给定的图的 (K) 阶线图是欧拉图 , 那么 ((K - 1)) 阶线图必然每个点的度数都奇偶性相同。
接着 , 若 (K) 阶线图的度数奇偶性相同 , 将 ((K - 1)) 阶线图奇数度数的点放在左侧 , 偶数的点放在右侧 , 那么这张图必然是二分图。 而二分图不可能是任何图的线图。
综上得到了判定的方法 , 但具体实现还需考虑一条链的情况 , 因为一条 包含 (K) 个点的链求 (K) 次线图最终必然会成为一个点。
时间复杂度 :(O(N alpha(N)))
(B)
考虑容斥原理 , 两个矩形相交的条件为 :
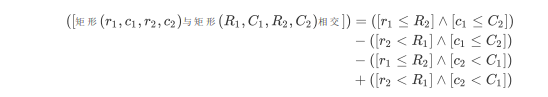
发现这些贡献是二维偏序。 考虑整体二分 , 每次用树状数组求二维偏序即可。
时间复杂度 : (O((N + M)log^2N))