【POJ 1804】 Brainman

【题目链接】

          点击打开链接

【算法】

          本题是一个很经典的问题 ： 归并排序求逆序对数，可以用分治算法解决

          分治，分而治之，分治算法的思想就是将一个问题转化为若干个子问题，对这些子问题分别求解，最后，

          通过子问题的答案反推得到总的答案

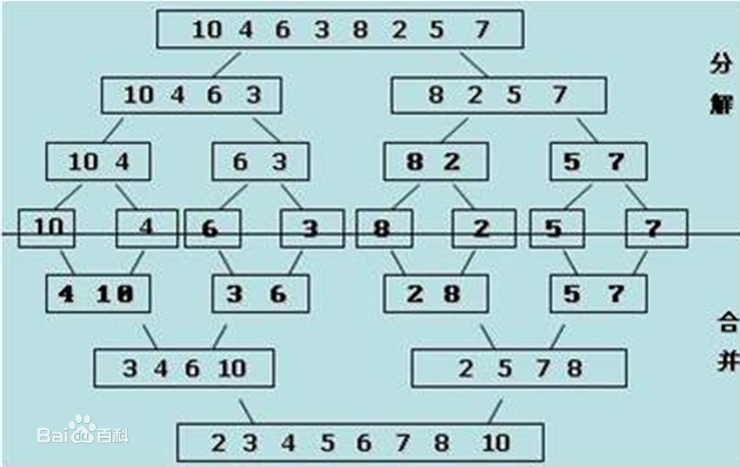
          通过归并排序求逆序对数的算法流程图如下 ：

         

【代码】

             

#include <algorithm>
#include <bitset>
#include <cctype>
#include <cerrno>
#include <clocale>
#include <cmath>
#include <complex>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <ctime>
#include <deque>
#include <exception>
#include <fstream>
#include <functional>
#include <limits>
#include <list>
#include <map>
#include <iomanip>
#include <ios>
#include <iosfwd>
#include <iostream>
#include <istream>
#include <ostream>
#include <queue>
#include <set>
#include <sstream>
#include <stdexcept>
#include <streambuf>
#include <string>
#include <utility>
#include <vector>
#include <cwchar>
#include <cwctype>
#include <stack>
#include <limits.h>
using namespace std;
#define MAXN 1010

int i,T,n,ans;
int a[MAXN];
 
inline void init()
{
        int i;
        ans = 0;
        scanf("%d",&n);
        for (i = 1; i <= n; i++) scanf("%d",&a[i]);    
}
inline void _merge(int l,int r)
{
        int i;
        int mid = (l + r) >> 1;
        int t1 = l,t2 = mid + 1; 
        int len = 0;
        static int tmp[MAXN];
        while (t1 <= mid && t2 <= r)
        {
                if (a[t1] <= a[t2])
                {
                        tmp[++len] = a[t1];
                        ans += t2 - mid - 1;
                        t1++;
                } else
                {
                        tmp[++len] = a[t2];
                        t2++;
                }
        }
        while (t1 <= mid)
        {
                tmp[++len] = a[t1];
                t1++;
                ans += r - mid;
        }
        while (t2 <= r)
        {
                tmp[++len] = a[t2];
                t2++;
        }
        for (i = 1; i <= r - l + 1; i++) a[l+i-1] = tmp[i];
}
inline void merge_sort(int l,int r)
{
        int mid;
        if (l == r) return;
        else
        {
                mid = (l + r) >> 1;
                merge_sort(l,mid);
                merge_sort(mid+1,r);
        }
        _merge(l,r);
}
int main() {
        
        scanf("%d",&T);
        for (i = 1; i <= T; i++)
        {
                init();
                merge_sort(1,n);
                printf("Scenario #%d:
",i);
                printf("%d

",ans);    
        }
        
        return 0;
    
}