二叉树的线索化

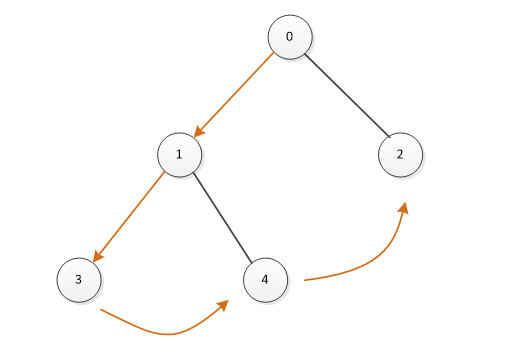
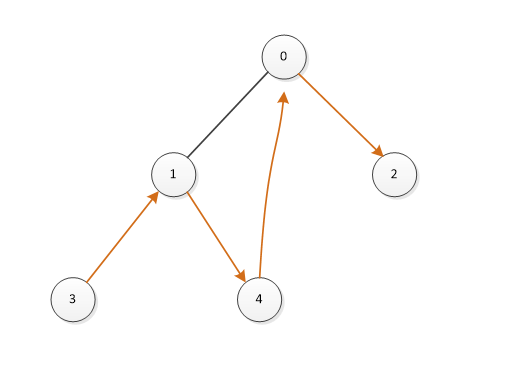
二叉树是一种非线性结构，遍历二叉树几乎都是通过递归或者用栈辅助实现非递归的遍历。二叉树作为存储结构时，一个节点只能获取节点的左孩子和右孩子，不能直接得到节点的任一遍历序列的前驱或者后继。为了保存这种在遍历中需要的信息，我们利用二叉树中指向左右子树的空指针来存放节点的前驱或后继信息。

也就是说，线索二叉树就是充分利用二叉树节点中的空指针，让它们分别指向本节点的前驱或者后继。既充分利用了资源，又方便我们遍历这颗二叉树。

1、线索二叉树的概念

n个节点的二叉树中含有n+1个空指针域。利用二叉树中的空指针域 来存放在某种遍历次序下的前驱和后继 ，这种指针叫“线索”。这种加上了线索的二叉树称为线索二叉树（Threaded BinaryTree）。根据遍历次序的不同，线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。

2、线索二叉树结构定义

/*线索化二叉树的结构*/
enum Flag
{
    LINK,
    CLUE
};

struct TreeNode
{
    TreeNode(int x) : value(x), left(NULL), right(NULL), left_flag(LINK), right_flag(LINK) {};
    int value;
    TreeNode *left;
    TreeNode *right;
    Flag left_flag;
    Flag right_flag;
};

value

left

left_flag

right

right_flag

 3、前序线索二叉树实现

/*前序遍历的构建*/
void prevCreate(TreeNode *root, TreeNode *&prev)  //&prev用引用，相当于全局变量的作用，在整个递归过程传递  
{
    if(root)
    {
        if(root->left == NULL)
        {
            root->left_flag = CLUE;
            root->left = prev;
        }
        if(prev && prev->right == NULL)
        {
            prev->right_flag = CLUE;
            prev->right = root;
        }
        prev = root;
        if(!root->left_flag)
        {
            prevCreate(root->left, prev);
        }
        prevCreate(root->right, prev);
    }
}



/*前序线索下的遍历*/
void prevOrder(TreeNode *root)
{
    while(root)
    {
        while(root->left_flag != CLUE)
        {
            cout << root->value << " ";
            root = root->left;
        }
        cout << root->value << " ";
        root = root->right;
    }
    cout << endl;
}

 4、中序线索二叉树实现

/*中序遍历的构建*/
void inCreate(TreeNode *root, TreeNode *&prev)
{
    if(root)
    {
        inCreate(root->left, prev);
        if(root->left == NULL)
        {
            root->left_flag = CLUE;
            root->left = prev;
        }
        if(prev && prev->right == NULL)
        {
            prev->right_flag = CLUE;
            prev->right = root;
        }
        prev = root;
        inCreate(root->right, prev);
    }
}



/*中序线索下的遍历*/
void inOrder(TreeNode *root)
{
    while(root)
    {
        while(root->left_flag != CLUE)
            root = root->left;
        cout << root->value << " ";
        while(root->right_flag != LINK)
        {
            root = root->right;
            cout << root->value << " ";
        }
        root = root->right;
    }
    cout << endl;
}

 5、线索化思想拓展

题目：如何将一个二叉树转化成一个有序的双向链表？

在没有学线索化之前，这道题可能非常麻烦。但现在，利用中序线索化的思想就可以很快将这道题做出来！

/*利用中序线索化思想将二叉树转换成有序的双向链表*/
void TreeToList(TreeNode *root)
{
    static TreeNode *prev = NULL;  //设立prev保存上一次访问的节点
    if(root == NULL)               //根节点为空，直接返回
        return;
    TreeToList(root->left);        //递归左子树
    root->left = prev;             //让左指针指向上一次访问的节点，即前驱
    if(prev)
        prev->right = root;        //让prev指向当前节点，构成双向
    prev = root;                   //更新prev
    TreeToList(root->right);       //递归右子树
}

本博文参考https://www.cnblogs.com/shihaochangeworld/p/5473163.html