什么是二叉排序树?二叉排序树和二叉树有什么关系呢?结合图像,让我们一点点来学习~
首先要明确的是二叉排序树是查找中运用很多的动态查找表,关于动态查找和静态查找,我们这次只是点明一点点,具体的部分下次再讲~
所谓动态查找,就是表在查找过程中动态生成我们所需要的表啦:

那么二叉排序树又是动态查找表中比较厉害(雾)的一种。。。
那么,二叉排序树有什么特点呢?

因此我们可以了解到,二叉排序树仍然具有树的特点,同时它的内部子树仍然保持高度有序呢(单个节点拎出来仍然是一颗二叉排序树)!
既然是树,最有效的存储方式当然是链表了~
按照链表定义,轻松写出结构体:
typedef struct BiNode { int data; BiNode *lchild=NULL; BiNode *rchild=NULL; }BiNode,*BiTree;//声明一棵树,以后可以使用
这里的结构体对左右孩子的声明还有一种写法:
struct BiNode *lchild=NULL; struct BiNode *rchild=NULL;
既然是一棵树,接下来自然需要插入来生成了,但是我们需要注意,二叉排序树由于高度有序,插入的方式自然不同,我们认为最好是需要是对叶节点进行操作是最理想的状态,为了达到我们的目的,我们需要写一个遍历函数:
bool SearchTree(BiTree T,int kval,BiTree f,BiTree &tmp)//树的查找,这里思考了很久tmp的作用,最后理解为之后有时会需要这节点来干一些神奇的事情 { if(!T)//如果是空树,那么自然查不到了 { tmp=f; return false; } else { if(T->data==kval)//如果此节点对应数据恰好吻合,bingo { tmp=T; return true; } else if(kval< (T->data)) SearchTree(T->lchild,kval,T,tmp);//这里的遍历查找自然不必多说 else SearchTree(T->rchild,kval,T,tmp); } }

我们能够对叶节点进行操作的话,自然可以用递归的方式进行新节点的插入操作,由于二叉排序树需要左边小于当前节点而右边大于当前节点,我们需要仔细考虑判断条件:

话不多说,上代码:
void CreatTree(BiTree &T,int data)//树的建立,非常简单,不必过多注释 { BiTree tmp; if(!SearchTree(T,data,NULL,tmp))//这里是一定需要遍历到最下面的叶节点的,不然插入节点是一件非常麻烦的事情 { BiNode *t=new BiNode; t->data=data; if(!tmp) T=t; else if(data< (tmp->data)) tmp->lchild=t;//若当前数据小于节点,自然插入左边啦 else tmp->rchild=t; cout << "Insert successful" << endl; } else cout << "Insert failed" << endl; }
我们成功的插入了新的叶节点,是否意味着我们的工作完成了2/3呢,不幸的是,节点的删除工作十分繁琐,需要考虑的情况非常多,对于叶节点的删除是一件简单的事情,而对于中间节点:删除之后依然保留二叉排序树的高度有序是一件非常麻烦的事情,好在前人已经帮我们整理好了我们需要考虑的情况:

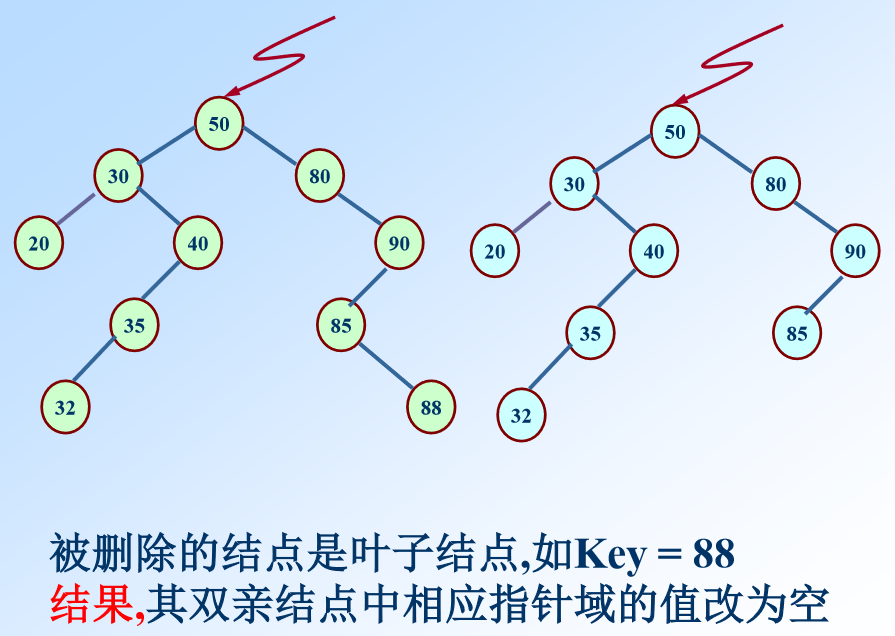


那么,上代码:
void Delete(BiTree &p) { BiTree q; BiTree s; //从树中删除节点p //重新连接左右子树 if(!p->rchild)//如果右兄弟那棵树是空的 { q = p->lchild;//这里跳过了当前节点,走向了下一个左子女 p->data = q->data;//这里把下一个节点的数据存到了当前节点 p->rchild = q->rchild;//这里把下一个节点的左右子女兄弟均转移到了当前节点上, p->lchild = q->lchild;//即把下面的那一棵树变成了当前的节点 free(q);//转移完成,删除"中转站" } else if(!p->lchild)//如果左子女那棵树是空的,这里的操作和上面没有区别,只是对左右的树的操作反过来了 { q = p->rchild; p->data = q->data; p->rchild = q->rchild; p->lchild = q->lchild; free(q); } else if(p->lchild&&p->rchild)//如果左右都有树的情况下,这种情况比较复杂 { q = p;//复制p到q,这样会得到两个一模一样的树(当前节点的下面整体) s = p->lchild;//s作为“中转站”,得到p左子女的那棵树 while (s->rchild)//遍历p左子女的右边兄弟(较大的数字)当然也可以说是第一个后继 { q = s;//把q更新为p左子女的后继的前一个节点 s = s->rchild;//持续循环的条件 } p->data = s->data;//把p的关键字更新为它的左子女的第一个后继 if (q != p)//这里代表成功更新,也就是p的左子女有了后继 { q->rchild = p->lchild;//这里的操作比较复杂:首先由于现在的大节点的数据更新为原先的左子女的第一个后继,那么他就可以访问此后继的左子女 }//由于是第一个后继,那么一定没有右兄弟了! else//更新失败,那么回到第二种右兄弟为空树的情况(好麻烦==||) { q->lchild = s->lchild; } free(s);//最后依然是需要删除新建的树呢~ } } void DeleteTree(BiTree &T,int data) { if(!T) cout << "can't delete this data!" << endl; else { if(data==T->data)//如果此(当前找到的节点是要删除的节点) { Delete(T); cout << "delete this data successful!" << endl; } else if(data< (T->data)) DeleteTree(T->lchild,data); else DeleteTree(T->rchild,data);//这里用的遍历的查找方式 } }
注释已经把我想说的话说完啦~~
最后我们需要验证一下我们的数据结构是否能够经受考验:
#include <bits/stdc++.h> using namespace std; typedef struct BiNode { int data; BiNode *lchild=NULL; BiNode *rchild=NULL; }BiNode,*BiTree;//声明一棵树,以后可以使用 bool SearchTree(BiTree T,int kval,BiTree f,BiTree &tmp)//树的查找,这里思考了很久tmp的作用,最后理解为之后有时会需要这节点来干一些神奇的事情 { if(!T)//如果是空树,那么自然查不到了 { tmp=f; return false; } else { if(T->data==kval)//如果此节点对应数据恰好吻合,bingo { tmp=T; return true; } else if(kval< (T->data)) SearchTree(T->lchild,kval,T,tmp);//这里的遍历查找自然不必多说 else SearchTree(T->rchild,kval,T,tmp); } } void CreatTree(BiTree &T,int data)//树的建立,非常简单,不必过多注释 { BiTree tmp; if(!SearchTree(T,data,NULL,tmp))//这里是一定需要遍历到最下面的叶节点的,不然插入节点是一件非常麻烦的事情 { BiNode *t=new BiNode; t->data=data; if(!tmp) T=t; else if(data< (tmp->data)) tmp->lchild=t;//若当前数据小于节点,自然插入左边啦 else tmp->rchild=t; cout << "Insert successful" << endl; } else cout << "Insert failed" << endl; } void Display(BiTree T)//先序遍历展示是否插入成功! { if(T) { cout << T->data << ' ' ;//递归show结果自然不必多说 Display(T->lchild); Display(T->rchild); } } void Delete(BiTree &p) { BiTree q; BiTree s; //从树中删除节点p //重新连接左右子树 if(!p->rchild)//如果右兄弟那棵树是空的 { q = p->lchild;//这里跳过了当前节点,走向了下一个左子女 p->data = q->data;//这里把下一个节点的数据存到了当前节点 p->rchild = q->rchild;//这里把下一个节点的左右子女兄弟均转移到了当前节点上, p->lchild = q->lchild;//即把下面的那一棵树变成了当前的节点 free(q);//转移完成,删除"中转站" } else if(!p->lchild)//如果左子女那棵树是空的,这里的操作和上面没有区别,只是对左右的树的操作反过来了 { q = p->rchild; p->data = q->data; p->rchild = q->rchild; p->lchild = q->lchild; free(q); } else if(p->lchild&&p->rchild)//如果左右都有树的情况下,这种情况比较复杂 { q = p;//复制p到q,这样会得到两个一模一样的树(当前节点的下面整体) s = p->lchild;//s作为“中转站”,得到p左子女的那棵树 while (s->rchild)//遍历p左子女的右边兄弟(较大的数字)当然也可以说是第一个后继 { q = s;//把q更新为p左子女的后继的前一个节点 s = s->rchild;//持续循环的条件 } p->data = s->data;//把p的关键字更新为它的左子女的第一个后继 if (q != p)//这里代表成功更新,也就是p的左子女有了后继 { q->rchild = p->lchild;//这里的操作比较复杂:首先由于现在的大节点的数据更新为原先的左子女的第一个后继,那么他就可以访问此后继的左子女 }//由于是第一个后继,那么一定没有右兄弟了! else//更新失败,那么回到第二种右兄弟为空树的情况(好麻烦==||) { q->lchild = s->lchild; } free(s);//最后依然是需要删除新建的树呢~ } } void DeleteTree(BiTree &T,int data) { if(!T) cout << "can't delete this data!" << endl; else { if(data==T->data)//如果此(当前找到的节点是要删除的节点) { Delete(T); cout << "delete this data successful!" << endl; } else if(data< (T->data)) DeleteTree(T->lchild,data); else DeleteTree(T->rchild,data);//这里用的遍历的查找方式 } } int main() { BiTree T=NULL; cout << "Please input the number n of the Bstree:" ; int n; cin>> n; int data; cout << "Please input the key of the Bstree" << endl; for(int i=0;i<n;i++) { cin>> data; CreatTree(T,data); } cout << "Please input a key to Search:" ; int kval; cin>> kval; BiTree tmp; if(SearchTree(T,kval,NULL,tmp)) cout << "the data is found!" << endl; else cout << "can't search this data!" << endl; Display(T); cout << endl; cout << "input the key data you want to delete:" ; int key; cin>> key; DeleteTree(T,key); Display(T); return 0; }
以上!
二叉排序树的相关内容就是这些啦~~
希望大家能够多多指教,本弱鸡知道和大佬们差距很大,希望大家看到博主的错误能够和博主探讨一波,带带本弱鸡一起进步叭!
感谢大家!