快速傅里叶变换（FFT）求解多项式乘法

在我还会FFT的时候赶快写下一篇博客留着以后看。。。。。。

FFT是用来求解多项式乘法，那么首先我们要知道多项式是啥。

[A(x) = a_0+a_1x^1+a_2x^2+···+a_{n-1}x^{n-1} ]

这是个n-1次多项式（最高项是(x^{n-1})），(a_0,a_1,···a_{n-1})是它各项的系数，该多项式可以写成：

[A(x) = sum_{j=0}^{n-1}a_jx^j ]

一个多项式可以通过一组系数所确定，而这组系数所组成的向量也叫做系数向量（如(A(x))的系数向量为：[(a_0 a_1 ··· a_{n-1})]），通过系数向量表示一个多项式的方式叫做系数表示法

多项式乘法就是，我们已知两个多项式：(A(x),B(x))，分别是n-1次和m-1次多项式。

[A(x) = sum_{j = 0}^{n - 1}a_jx^j\ B(x) = sum_{j = 0}^{m-1}b_jx^j ]

现在讲这两个多项式相乘，得到一个最高n+m-1次多项式：

[C(x) = sum_{j = 0}^{n+m-1}c_jx^j ]

那么求解(C(x))也就是求出它的系数向量：[(c_0 c_1 ··· c_j ··· c_n+m-1)]

如果直接遍历(A(x),B(x))的每一项的话是(O(n*m))，我们需要更快的算法，就是我们所讨论的：快速傅里叶变换(FFT)

前置芝士：

点值表示法

对于一个已知的多项式(A(x))，将(x_0)代入可以得到一个确定的(y_0)，并且，可以将((x_0,y_0))看做是坐标系上的一个点。进一步可以将任意多的互不相等的自变量代入((x_1,x_2,···))，从而得到更多的点：((x_1,y_1),(x_2,y_2),···)

我们知道，通过两个（不同的）点，可以解析一次多项式((ax+b))，通过三个不同的点可以解析二次多项式((ax^2+bx+c))，所以可以进一步的推出，通过n+1个不同的点，可以解出n次多项式

通过n+1个不同的点(left{ (x_1,y_1),(x_2,y_2),··· ight})，唯一确定一个n次多项式，该方式也叫做多项式的点值表示法

我们惊奇的发现两个用点值表示的多项式相乘，复杂度是(O(n))的！具体方法：(C(x_i)=A(x_i)×B(x_i))，所以O((n))枚举(x_i)即可。

要是我们把两个多项式转换成点值表示，再相乘，再把新的点值表示转换成多项式岂不就可以(O(n))解决多项式乘法了！

……很遗憾，显然，把多项式转换成点值表示的朴素算法是(O(n^2))的。另外，即使你可能不会——把点值表示转换为多项式的朴素“插值算法”也是(O(n^2))的。

但是可以发现，大整数乘法复杂度的瓶颈可能在“多项式转换成点值表示”这一步（以及其反向操作），只要完成这一步就可以(O(n))求答案了。如果能优化这一步就可以了。

于是乎介绍另外两个前置芝士

离散傅里叶变换（DFT）以及离散傅里叶变换逆变换（IDFT），公式如下：

[X_k = sum_{j = 0}^{n-1}x_je^{frac{2pi i}{n}kj} (DFT)\ X_j = frac{1}{n}sum_{k = 0}^{n-1}X_ke^{frac{-2pi i}{n}jk}(IDFT) ]

上面的两个式子中(i)是虚根（(i^2 = -1)），关于这两个式子的证明在文章最后会给出。

我们设置一些变量，将这两个公式代入到我们之前的问题里。

设：(w = e^{frac{2pi i}{N}})，其中(N = n+m)，关于变量(w)的性质先不讨论，之后会有，再令

[c_j = f(j),C_k = C(w^k) ]

将这些变量代入到DFT的公式里可得到：

[C_k = C(w^k)=sum_{j = 0}^{N-1}c_j(w^k)^j= sum_{j=0}^{N-1}c_je_{frac{2pi i}{N}kj} ]

通过上式讲DFT与我们目标多项式(C(x))关联了起来，自然也就可以通过IDFT来计算多项式的系数(c_j)：

[c_j = frac{1}{N}sum_{k=0}^{N-1}C_k(w^{-j})^k=frac{1}{N}sum_{k=0}^{N-1}C_ke^{-frac{2pi i}{N}jk} ]

但是，由于不知道(c_j)的具体值（知道就完结撒花了），所以无法用DFT计算(C(w^k))

不过，我们知道：(C(x)=A(x)*B(x))，而且多项式(A(x)B(x))的系数是已知的，所以可以“曲线救国”：

[C(w^k)= A(w^k)*B(w^k) ]

通过该式计算(C(w^k))，然后再使用IDFT计算(c_j)。

以上是FFT的概括，下面进行展开讨论

一个芝士：N次单位根

为了更好的讨论(w = e^{frac{2pi i}{N}})，我们还是从欧拉公式说起

[e^{i heta} = cos heta+isin heta ]

该公式的证明也在文章最后给出。

(e^{i heta})是一个复数，他的实部的值为(cos heta)，虚部的值为(sin heta)，所以，(e^{i heta})对应复数平面上的点与原点之间的距离恒为1，如图

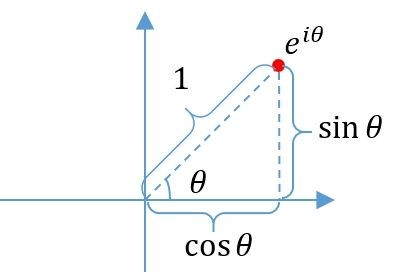
因为(sin heta,cos heta)是周期函数（周期为(2pi)），所以可以得出：

[e^{i( heta+2pi)=e^{i heta}} ]

并且无论( heta)取何值，(e^{i heta})都是分布在复平面的单位圆上，由于是单位元，所以( heta)此时就等于是从1（起点）到(e^{i heta})在圆上的弧长。

上面简要介绍了欧拉公式，下面回到我们定义的变量：(w = e^{frac{2 pi i}{n}})，前面的概述中为了方便，(w)没有加上下标，在此为更清楚的表示会给(w)加一个下标：(w_n=e^{frac{2pi i}{n}})

从面欧拉公式的讨论中可以指导，(e^{2pi i} = 1)，相当于在单位圆上绕了一圈又回到了起点，而(frac{2pi}{n})相当于是这个单位圆分成了(n)等分，而(w_n^k)就对应单位圆上第(k)个等分点（(k=0,1,2,···，n-1)）

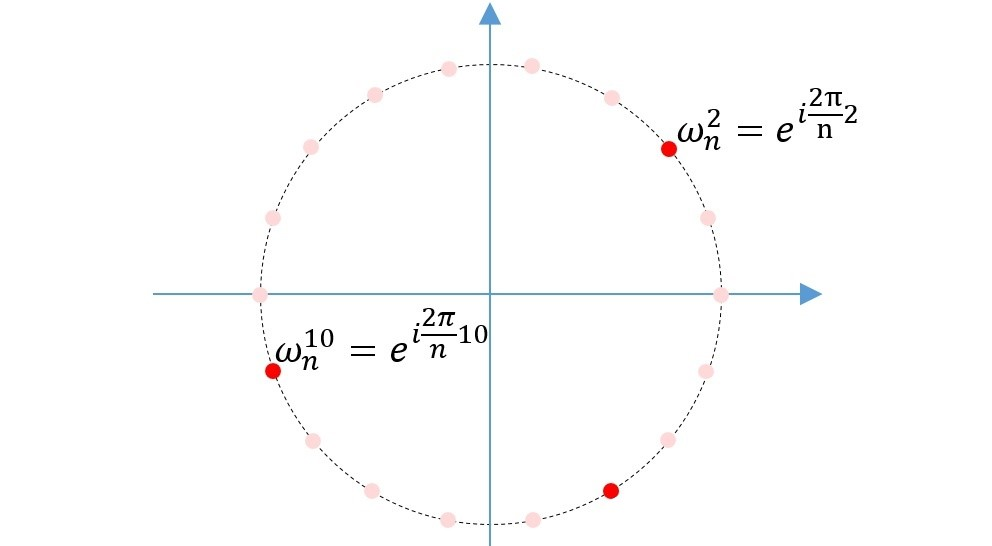
这是个(n=18)的例子，并标出了两个值(left{ w_n^k|k=2,10 ight})，通过前面的讨论以及这个栗子，应该对(w_n^k)有了一个比较直观的认识，说了这么多，应该能猜到N次单位根就是指的它了，关于N次单位根介绍几个性质：

[1. w_n^{k+frac{n}{2}}=e^{frac{2pi i}{n}(k+frac{n}{w})}=e^{frac{2pi i}{n}k}e^{ipi} =w_n^k(cospi+isinpi)=-w_n^k \2. w_{2n}^{2k} = w_n^k \3. w_n^{-k} = 1·e^{frac{i2pi}{n}(-k)} = e^{2pi i}e^{frac{2 pi i}{n}(-k)}=e^{frac{2pi i}{n}(n-k)}=w_n^{n-k} ]

性质1是消去引理，性质2是折半引理，性质3我忘了叫啥。。。

计算(C(w_N^k))

首先，定义(N = m+n)（n,m分别是多项式(A(x),B(x))的系数数量），前面已经说过无法直接使用DFT计算(C(w_n^k))，需要先计算(A(w_N^k),B(w_N^k))

单数如果直接把(left{ w_N^k|k=0,1,2,···，N-1 ight})简单粗暴的代进去，时间复杂度依旧是(O(N^2))，无论后面如何计算，也无法降低整个算法的复杂度，因为，需要使用的一些方法，来降低(A(w_N^k),B(w_N^k)) 的时间

for example，我们有个多项式：

[H(x) = h_0+h_1x^1+h_2x^2+h_3x^3 ]

我们可以将它的奇数项与偶数项分开：

[H(x)=(h_0+h_2x^2)+(h_1x^1+h_3x^3)=(h_0+h_2x^2)+x(h_1+h_3x^2)\= H1(x^2)+xH2(x^2) ]

并且(H1(x),H2(x))还可以递归的计算下去，该方法用到(A(x),B(x))上就是：

[A(x) = A1(x^2)+xA2(x^2)B(x) = B1(x^2)+xB2(x^2) ]

时间复杂度就变成了：

[T(n) = 2T(frac{n}{2})+O(n)=O(nlogn) ]

除此之外，还可以利用前面讨论的单位根的性质来降低计算量，例如，(0 leq k < frac{n}{2})：

[A(w_n^k) = A1(w_n^{2k})+w_n^kA2(w_n^{2k})=A1(w_{frac{n}{2}}^k)+w_n^kA2(w_{frac{n}{2}}^k)\A(w_n^{k+frac{n}{2}}) = A1(w_n^{2k+n})+w_n^{k+frac{n}{2}}A2(w_n^{2k+n}) = A1(w_n^{2k})-w_n^kA2(w_n^{2k}) \= A1(w_{frac{n}{2}}^k)-w_n^kA2(w_{frac{n}{2}}^k)) ]

这样，计算(k)一般的取值范围就可以得到整个取值范围的结果，所以，将(A(w_N^k),B(w_N^k))计算完毕之后，就可以通过简单的乘法来计算(C(w_N^k))：

[C(w_N^k) = A(w_N^k)B(w_N^k),k=0,1,2,···，N-1 ]

求解(C(x))系数

计算 这一步基本已经完成一大半了，只需要使用IDFT公式来求解(C(x))的各项系数就可以了：

[c_j = frac{1}{N}sum_{k=0}^{N-1}C_ke^{-frac{2pi i}{N}jk} = frac{1}{N}sum_{k=0}^{N-1}C_k(e^{-frac{2pi i}{N}j})^k=frac{1}{N}sum_{k=0}^{N-1}C_k(w_N^{-j})^k ]

上面式子中(C_k = C(w_N^k))，另外，为了方面表示，通常会构造一个N-1次多项式(D(x))，它的系数就是各个(C_k)的值：

[D(x) = C_0 + C_1x^1+C_2x^2+···+C_{N-1}x^{N-1} = sum_{k=0}^{N-1}C_kx^k ]

所以，最终(c_j)的计算公式可以写成：

[c_j = frac{1}{N}sum_{k=0}^{N-1}C_k(w_N^{-j})^k=frac{1}{N}sum_{k=0}^{N-1}C_k(w_N^{N-j})^k=frac{1}{N}D(w_N^{N-j}) ]

上式第二部使用了单位根的性质3：

[c_0 = frac{1}{N}D(w_N^{N-0}) = frac{1}{N}D(w_N^N)=frac{1}{N}D(w_N^0) ]

总结

1.取N个单位根：[(w_N^0 w_N^1 w_N^2 ··· w_N^{N-1})]

2.将它们分别代入到多项式(A(x),B(x))中

3.计算(C(w_N^k) = A(w_N^k)B(w_N^k))

4.构造一个新的多项式(D(x) = C_0+C_1x^1+C_2x^2+···+C_{N-1}x^{N-1})

5.计算(D(w_N^k))

6.计算多项式(C(x))的系数(c_j=frac{1}{N}D(w_N^{N-j}),j=0,1,2,···，N-1)

at last（未完待续）

• 欧拉公式证明
• DFT与IDTF证明