给定一个正整数数列,和正整数 p,设这个数列中的最大值是 M,最小值是 m,如果 M≤mp,则称这个数列是完美数列。
现在给定参数 p 和一些正整数,请你从中选择尽可能多的数构成一个完美数列。
输入格式:
输入第一行给出两个正整数 N 和 p,其中 N(≤105)是输入的正整数的个数,p(≤109)是给定的参数。第二行给出 N 个正整数,每个数不超过 109。
输出格式:
在一行中输出最多可以选择多少个数可以用它们组成一个完美数列。
输入样例:
10 8 2 3 20 4 5 1 6 7 8 9
输出样例:
8
1.使用二分法O(nlogn),n=10-5,
#include<cstdio> #include<algorithm> #include<cmath> using namespace std; int a[100010],n,m; int binarySearch(int i,long long x){ if(a[n-1]<=x) return n; int l=i+1,r=n-1,mid; while(l<r){ mid=(l+r)/2; if(a[mid]<=x) l=mid+1; else r=mid; } return l; } int main(){ scanf("%d%d",&n,&m); for(int i=0;i<n;i++) scanf("%d",&a[i]); sort(a,a+n); int maxx=0; for(int i=0;i<n;i++){ int low=binarySearch(i,(long long)a[i]*m); maxx=max(maxx,low-i); } printf("%d",maxx); return 0; }
2.使用STL函数简化代码
#include<cstdio> #include<algorithm> #include<cmath> using namespace std; int a[100010]; int main(){ int n,m; scanf("%d%d",&n,&m); for(int i=0;i<n;i++) scanf("%d",&a[i]); sort(a,a+n); int maxx=0; for(int i=0;i<n;i++){ int low=upper_bound(a+i+1,a+n,(long long) a[i]*m)-a; maxx=max(maxx,low-i); } printf("%d",maxx); return 0; }
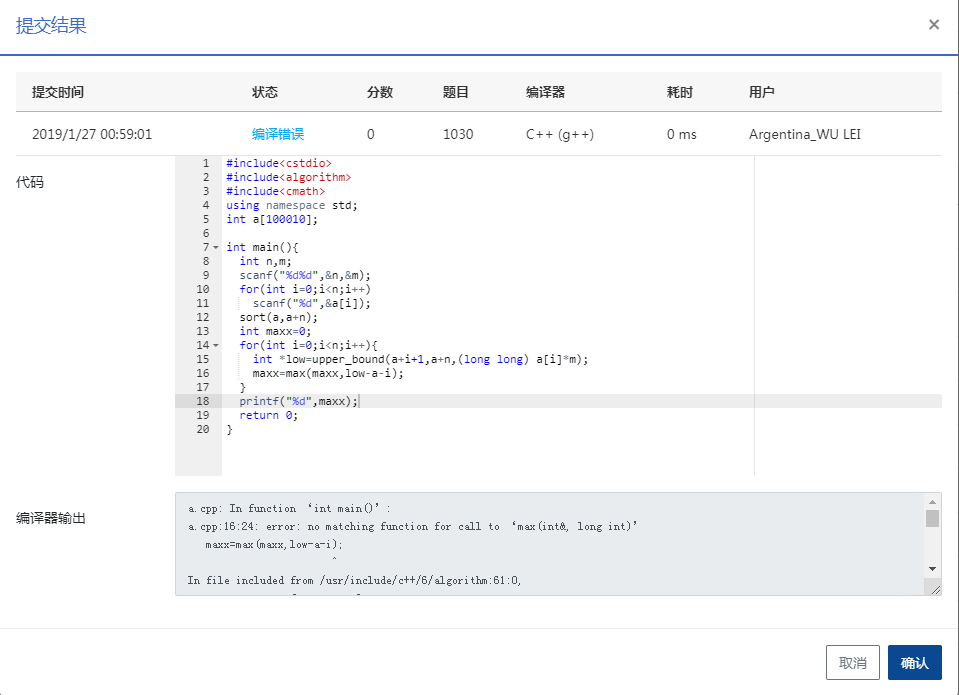
注意此处upper_bound返回的是*int型,见以下错误:
int *low=upper_bound(a+i+1,a+n,(long long) a[i]*m); maxx=max(maxx,low-a-i);