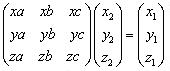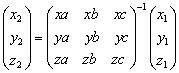坐标系的变换分两类:一类是坐标系中,点的位置不变,变的只是坐标的值,或者说改变的只是同一个点在不同系下的描述;二类是点的坐标值不改变,点的位置发生改变适应新的坐标系,或者说相同的坐标值在不同的坐标系中有不同的几何解释,从而得到不同的位置。
我们讨论的是前一种情况。
一)基底:
坐标系最根本的是基底,点P的坐标是(1,2,3)是什么意义?
可能说:表示的是P在直角坐标系中,在x轴上的投影为1,在y轴上的投影为2,在z轴上的投影为3。
对吗?
未必。
首先,我们讨论的未必是直角坐标系;
其次,所谓投影,一般是指作垂直的直线,这只有在直角坐标系中才是这样,在非直角坐标系中,作垂直是没有意义的,应该是“平行”。确定x轴上的分量要作与yoz平面平行的平面与x轴相交;
第三,在x轴上的分量未必为1,这只有在空间直角坐标系中当向量op=i+2j+3k时才是这样。
当向量op=i+2j+3k时,我们就叫点P的坐标为(1,2,3),这里的三个单位向量i,j,k就叫这个坐标系的基底。
但是要注意,坐标系的基底未必是向量i,j,k。
例:设有三个向量a,b,c,这三个向量未必是单位向量,也未必垂直,只是非常普通的三个向量,只要这三个向量非零且不共面,就可以作为基底,此时若向量op=a+2b+3c 则称点p在以a,b,c为基底的系下的坐标为(1,2,3)。
二)变换:
以向量i,j,k作为基底的坐标系(称原系)里一个点P(x1,y1,z1),即OP=x1*i+y1*j+z1*k。
设向量a=(xa,ya,za),即a=xa*i+ya*j+za*k;
向量b=(xb,yb,zb),即b=xb*i+yb*j+zb*k;
向量c=(xc ,yc,zc),即c=xc*i+yc*j+zc*k;
现以a,b,c为基底建立新系,则点P在新系下的坐标为多少?
设在新系下的坐标为(x2,y2,z2),则
向量op=x2*a+y2*b+z2*c
= x2*(xa*i+ya*j+za*k)+y2*(xb*i+yb*j+zb*k)+z2*(xc*i+yc*j+zc*k)
=(x2*xa+y2*xb+z2*xc)*i+(x2*ya+y2*yb+z2*yc)*j+(x2*za+y2*zb+z2*zc)*k
又OP=x1*i+y1*j+z1*k,
所以
x2*xa+y2*xb+z2*xc=x1
x2*ya+y2*yb+z2*yc=y1
x2*za+y2*zb+z2*zc=z1
写成矩阵形式
显然
同一个点位置不变,在新旧坐标系中有新旧两个坐标,这就是新旧两坐标的关系。
请再次回顾,并作观察,新坐标系的基底在原坐标系中的坐标为
向量a=(xa,ya,za);
向量b=(xb,yb,zb);
向量c=(xc ,yc,zc)。
三)应用:
在Polt3D中,在计算计算隐藏线面时,在一个x轴垂直电脑屏幕的坐标系(以向量i,j,k为基底,称Game系)中计算,但在表现出来,即给用户的感觉时,却用的是斜二侧画法使用的坐标系。
斜二测画法的坐标系(称Math系)基底为
向量a=(1,-0.35355334,-0.35355334)
向量b=(0,1,0);
向量c=(0,0,1)。
在计算旋转时,也要先放到Math系,GameToMath(p),再作旋转:Rotate(P),最后又回到Game系:MathToGame(P)。