引言
最大流问题
最大流问题就是一类解决有关于每条边有流量上限的问题。
就好像这样:
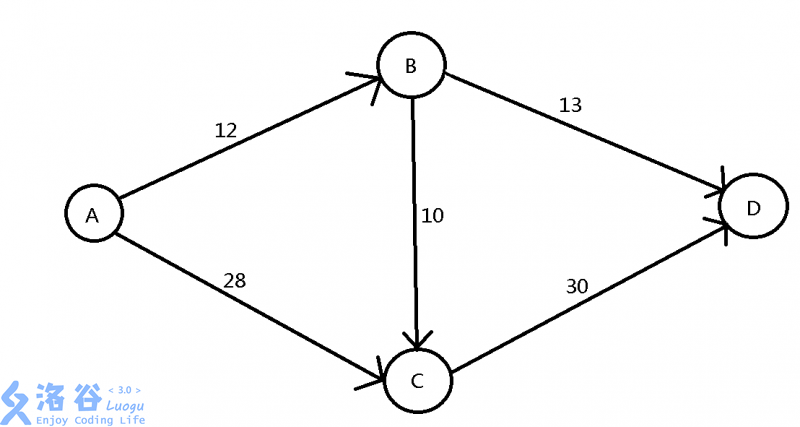
图中每条边上的数字叫做这条边的容量,它代表了最多能有多少个物品经过它。
而实际上有多少个物品经过这条边,我们把它称为物品的流量。
而起始点A称为源点,终点D称为汇点。
我们要解决的问题是,假设源点A有无数个物品,那么最多能有几个物品到达汇点。
最大流之Edmonds-Karp(EK)算法
1.实现方法
我们对于这样一道题,首先的思路就应该是经过多次搜索(最好使用BFS),每次都搜索一条源点到汇点的路径,而本次搜索到的结果就是路径上边的容量最小的边结果的和。这样最终一定能解决最大流的。
搜索的方式也非常简单。我们只需要每次运用bfs搜索一条路径,并且在搜索过的路径上都减去本次搜索到的边的容量的最小值。(注意:容量<=0的不可以继续使用)直到再也找不到源点到汇点的路径的时候,搜索就可以结束了。
算法的思路很简单,但是有一个很小的问题,那假如我们搜索到的路径不是最优路径,那怎么办?
我们也不可能回溯,那么这里要增加一个奇特的办法——————增加反向边。
具体的实现方法是:对于每一条边,刚开始增加一条容量为0的反向边,然后,每次正向边减去搜索到的最小值的时候,反向边就相应地增加搜索到的最小值就可以了。
这就是实现方法了。
PS:这段代码的思路叫增广路算法(定理),实现叫做EK算法。
2.思路
这个思路中主要有两个难理解的点。
2.1.为什么要在正向边减去搜索到的边的容量的最小值
这相当于已经是使用了这么多的流量,还剩下(当前容量-流量=如今容量)
2.2.为什么要在反向边增加搜索到的边的容量的最小值
这就要讲回刚刚那个很小的问题了。
我们为什么要增加反向边呢?这是因为我们相当于是让刚刚从正向边走过来的物品可以在通过这一条反向边回去。而想要让已经过来的物品回去,自然要增加一条反向边,相当于将刚刚的物品“退还”回去。
就像这样:
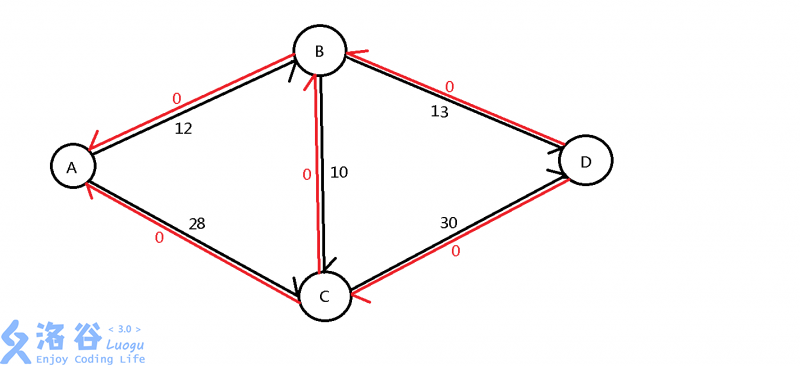
然后开始遍历。我们会发现最大流应该是A-B-D和A-C-D,它们加起来应该是40。
但如果第一次遍历到了A-B-C-D,第二次就只能遍历A-C-D,第三次就只能遍历A-B-D,总和只有32。
那怎么解决这个问题呢?
这就是反向边的用途了。
在遍历完A-B-C-D之后,再次遍历A-C-D,就会形成以下的图:
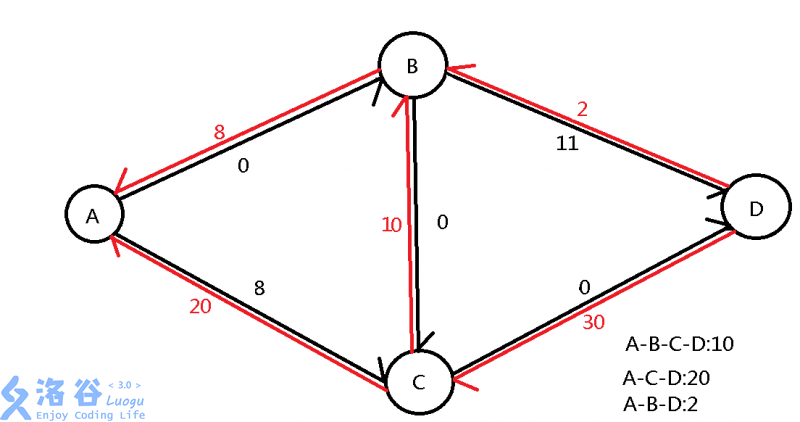
只需要再遍历一次A-C-B-D就可以了。
那为什么这么操作就可以了呢?
这就相当于从A-B来的物品将一部分应该属于A-C的物品的通道给占用了,所以说从A-B来的物品一定要留下同样多的通道来让A-C的物品通过,走原本属于A-B的通道。
大概就是这个意思(不会我也没有办法了)
3.代码
下面附上我用邻接表写的代码(丑陋的邻接表):
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int n,m,ans;
struct ed{
int u,c,f;
}d[201];
vector<ed>g[201];
bool bfs(){
bool vis[201]={};
queue<int>q;
vis[1]=true;
q.push(1);
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=0;i<g[x].size();i++){
int v=g[x][i].u;
int w=g[x][i].c;
if(w==0||vis[v])continue;
vis[v]=true;
q.push(v);
d[v].u=x,d[v].c=i;
if(v==n)return true;
}
}
return false;
}
int main(){
cin>>m>>n;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
g[u].push_back((ed){v,w,g[v].size()});
g[v].push_back((ed){u,0,g[u].size()-1});
}
while(bfs()){
int minn=0x3f3f3f3f;
for(int i=n;i!=1;i=d[i].u){
minn=min(minn,g[d[i].u][d[i].c].c);
}
for(int i=n;i!=1;i=d[i].u){
g[d[i].u][d[i].c].c-=minn;
g[i][g[d[i].u][d[i].c].f].c+=minn;
}
ans+=minn;
}
cout<<ans;
return 0;
}
4.EK算法小结
相信看到这里,你已经理解了EK算法的实现过程了(特别是反向边)。
但是:
事实上,读者无需搞清楚它们的原理,只需会使用即可。换句话说,可以把它们当作像STL一样的黑盒代码。
——————《算法竞赛入门经典》刘汝佳
而且:
虽然本节介绍了最大流的Edmonds-Karp算法,但在实践中一般不用这个算法,而是使用效率更高的Dinic或者ISAP算法。
——————《算法竞赛入门经典》刘汝佳
所以:EK算法其实没啥用
备注:有关Dinic和ISAP算法,会在下篇文章中讲到。
Dinic
咕咕咕
应用
最大流问题的经典应用——————二分图匹配
前言:有关二分图匹配
二分图匹配一共有两种解法,分别是匈牙利算法与最大流。
而它们两个虽然实现的方式不一样,但是它们都用到了同一个思想——————增广路
最大流相较于匈牙利算法来说稍微复杂了一(hen)点(duo)(所以说平常最好还是使用匈牙利算法吧),但是它可以解决某些匈牙利算法解决不了的问题(就像是有限制的二分图匹配问题)。
主要思路
我们只需要将边的容量改为1,并将源点连向第一部分的点,将第二部分的点连向汇点就可以了。
当然,我们现在还要跟据两道题来让大家理解如何才能解决特殊的二分图匹配问题。
吃饭
对于一道题来说,我们首先应该分析它需要什么算法。
这题需要我们将食物、饮料与奶牛分别配对,所以应该是二分图匹配。
对于二分图匹配,有匈牙利算法与最大流
然而,这道题需要我们将三种物品匹配,匈牙利算法无法解决。这时,我们需要用最大流。
对于一道用最大流解决的二分图匹配问题,最重要的问题有几个:
1.我们需要将什么进行配对
2.配对的顺序是什么
3.每条边的容量是什么(每两件要配对的物品的关系)
那我们怎么解决这几个问题呢(有些问题很好解决,直接在题目上就能找到。但是有些问题就需要我们的推理了,二分图匹配主要的难点就在这里(当然,由于二分图匹配代码较长,有时候调试程序也需要耐心))对于这几个问题,我们首先要列出需要注意的点。
这道题有几个需要注意的点。
1.每头奶牛只能吃1种食物和1种饮料
2.每种食物/饮料只能被一头奶牛吃一次
3.每头奶牛都只会吃固定的食物和饮料
我们就应该针对题目的这几个条件进行解题。
下面是这几个问题的解答:
1.由题意可知,我们需要将食物、饮料与奶牛配对。
2.这个问题是本题的难点,针对需要注意的点,我们可以得知
如果将奶牛放在最前或最后,那么就有可能会发生一种情况:
假设奶牛1吃食物1,喝饮料2,奶牛2吃食物1,喝饮料3,由于食物1和饮料3连在了一起,奶牛1就有可能在吃食物1的时候喝了饮料3。
所以我们应该将奶牛放在食物和饮料的中间。
3.每种食物/饮料只能被一头奶牛吃一次,所以边权应该都是1。
题目的分析到这里就结束了
吗?
这里还有一个问题:
假设奶牛1吃食物1,喝饮料1,它还吃食物2,喝饮料2。这样我们在遍历的时候就会让奶牛吃2种食物,喝2种饮料。
针对这种情况,我们会采用一种叫拆点的方法。
拆点就是将一个点拆成两个点并让两个点之间的边的容量限制经过这个点的流量。
所以,我们只需要将奶牛拆成两个,再把它们之间的边的容量为1就可以保证每头奶牛只能吃1种食物和1种饮料了。
题目的分析到这里才真正的结束了。
下面给出代码
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int n,m,k,h,ans;
struct ed{
int u,c,f;
}d[501];
vector<ed>g[501];
bool pd[501];
bool bfs(){
bool vis[501]={};
queue<int>q;
vis[0]=true;
q.push(0);
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=0;i<g[x].size();i++){
int v=g[x][i].u;
int w=g[x][i].c;
if(w==0||vis[v])continue;
vis[v]=true;
q.push(v);
d[v].u=x,d[v].c=i;
if(v==h)return true;
}
}
return false;
}
int main(){
cin>>n>>m>>k;
h=n+n+m+k+1;
for(int i=1;i<=n;i++){
int a,b,x,y;
cin>>a>>b;
if(a==0||b==0){
while(a--)cin>>x;
while(b--)cin>>y;
continue;
}
g[i].push_back((ed){i+n,1,g[i+n].size()});
g[i+n].push_back((ed){i,0,g[i].size()-1});
while(a--){
cin>>x;
x=x+n+n;
if(pd[x]==false){
pd[x]=true;
g[0].push_back((ed){x,1,g[x].size()});
g[x].push_back((ed){0,0,g[0].size()-1});
}
g[x].push_back((ed){i,1,g[i].size()});
g[i].push_back((ed){x,0,g[x].size()-1});
}
while(b--){
cin>>y;
y=y+n+n+m;
if(pd[y]==false){
pd[y]=true;
g[y].push_back((ed){h,1,g[h].size()});
g[h].push_back((ed){y,0,g[y].size()-1});
}
g[i+n].push_back((ed){y,1,g[y].size()});
g[y].push_back((ed){i+n,0,g[i+n].size()-1});
}
}
while(bfs()){
int minn=0x3f3f3f3f;
for(int i=h;i!=0;i=d[i].u){
minn=min(minn,g[d[i].u][d[i].c].c);
}
for(int i=h;i!=0;i=d[i].u){
g[d[i].u][d[i].c].c=g[d[i].u][d[i].c].c-1;
if(g[d[i].u][d[i].c].c<0){
g[d[i].u][d[i].c].c=0;
}
g[i][g[d[i].u][d[i].c].f].c+=minn;
}
ans+=minn;
}
cout<<ans;
return 0;
}
新年晚会
Description
N(3<=N<=200)头奶牛要办一个新年晚会。每头牛都会烧几道菜。一共有D(5<=D<=100)道不同的菜肴。每道菜都可以用一个1到D之间的数来表示。
晚会的主办者希望尽量多的菜肴能被带到晚会,但是每道菜的数目又给出了限制。
每头奶牛可以带K(1<=K<=5)道菜,但是必须是各不相同的(例如,一头牛不能带三块馅饼,但是可以带上一块馅饼,一份面包,和一些美味的桔子酱苜蓿)。
那么,究竟有多少菜可以被带来晚会呢?
Input
第一行包括三个整数N,K和D。
第二行有D个非负整数,表示每种菜可以带到晚会上的数目限制。
第三行到第N+2行,每行包括一个整数Z,表示一头牛可以准备的菜的道数;之后Z个整数,表示菜的标号,首先是第一种菜,然后是第二种菜,以此类推。
Output
仅一行一个整数,表示可以带到晚会上的最多的菜的数目。
Sample Input
4 3 5
2 2 2 2 3
4 1 2 3 4
4 2 3 4 5
3 1 2 4
3 1 2 3
Sample Output
9
对于这道题,我们还是使用跟上一题同样的推理方法(事实上,大多数最大流解决的二分图匹配问题都可以这么做)。
这道题要我们将奶牛与菜肴匹配,所以使用二分图匹配。
这道题有很多的限制,用匈牙利算法会比较麻烦,所以我们使用最大流。
这道题要注意的点有:
1.每道菜的数目被带到晚会的数量有限制
2.每头奶牛只能带k道菜
3.每头奶牛带的菜必须各不相同
接下来是对那三个问题的解答:
1.由题可知,是将奶牛与菜肴匹配
2.因为只有两个,所以顺序没有什么大的问题
3.这是本题的难点。因为每头奶牛只能带k道菜,所以源点到奶牛的边的容量应该是k;因为每头奶牛带的菜必须各不相同,所以奶牛与菜肴的边的容量应该是1;因为每道菜的数目有限制,所以菜肴与汇点的边的容量应该是限制的数目。
这道题也没有什么需要特别注意的点。所以题目分析到这里就结束了。
最后附上代码:
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int n,m,k,h,ans;
struct ed{
int u,c,f;
}d[501];
vector<ed>g[501];
bool bfs(){
bool vis[501]={};
queue<int>q;
vis[0]=true;
q.push(0);
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=0;i<g[x].size();i++){
int v=g[x][i].u;
int w=g[x][i].c;
if(w==0||vis[v])continue;
vis[v]=true;
q.push(v);
d[v].u=x,d[v].c=i;
if(v==h)return true;
}
}
return false;
}
int main(){
cin>>n>>k>>m;
h=n+m+1;
int x;
for(int i=n+1;i<=n+m;i++){
cin>>x;
g[i].push_back((ed){h,x,g[h].size()});
g[h].push_back((ed){i,0,g[i].size()-1});
}
for(int i=1;i<=n;i++){
int a;
cin>>a;
while(a--){
cin>>x;
x=x+n;
g[i].push_back((ed){x,1,g[x].size()});
g[x].push_back((ed){i,0,g[i].size()-1});
}
}
for(int i=1;i<=n;i++){
g[0].push_back((ed){i,k,g[i].size()});
g[i].push_back((ed){0,0,g[0].size()-1});
}
while(bfs()){
int minn=0x3f3f3f3f;
for(int i=h;i!=0;i=d[i].u){
minn=min(minn,g[d[i].u][d[i].c].c);
}
for(int i=h;i!=0;i=d[i].u){
g[d[i].u][d[i].c].c-=minn;
g[i][g[d[i].u][d[i].c].f].c+=minn;
}
ans+=minn;
}
cout<<ans;
return 0;
}