互评:图总结

1.思维导图

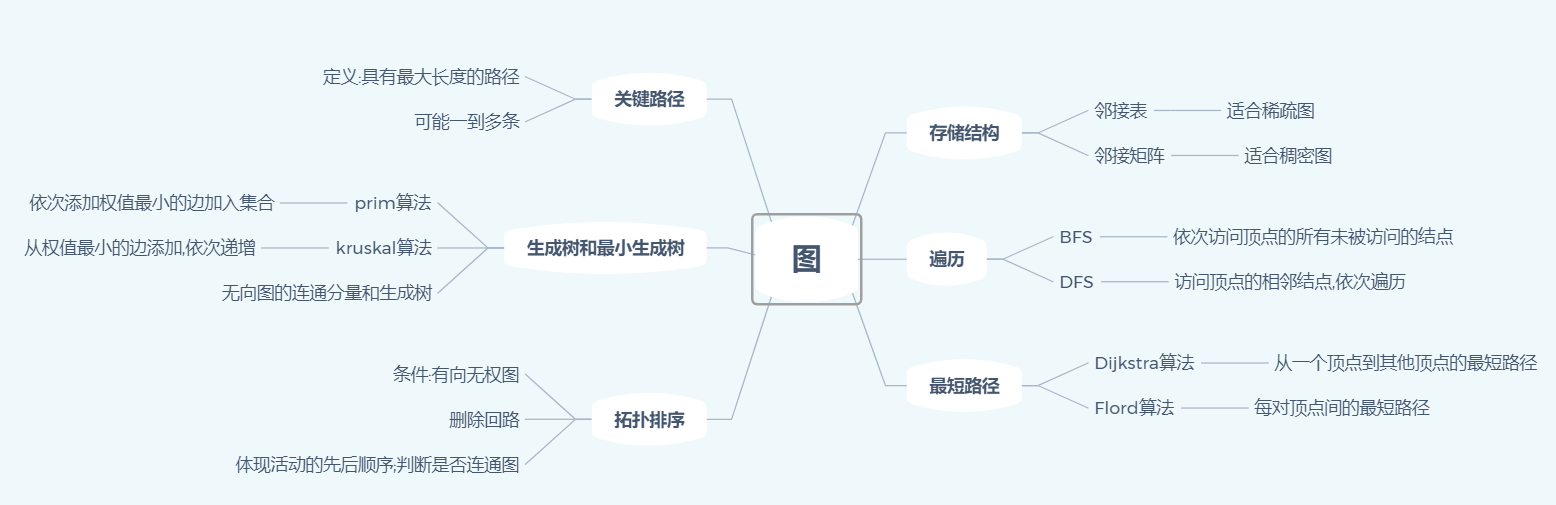
 2.重要概念的笔记(不求多但求精)

顶点的度:
有向图中，顶点的度=入度与出度的和
无向图中，顶点的度 =入度 = 出度

邻接表和邻接矩阵:
邻接表:想法:每个顶点都建立一个单链表存储,用来记录从该点出发的所有边的信息,第i个链表的第j个值即顶点i到j的权值
邻接表不唯一(边的输入次序和边结点的链接次序 不同);
邻接表适用于稀疏图
优点:查找任意一个顶点关联的所有边很快速
缺点:每次都要遍历各顶点的边表,耗时

邻接矩阵:想法:用一个二维数组A[i][j]保存i到j(边)的信息,A[i][j]的值即这条边的权值;

邻接矩阵是唯一的;

邻接矩阵存储法所占用的存储空间大小只与顶点个数有关，与图的边数无关;
邻接矩阵适用于稠密图
优点:时间复杂度比邻接表小
缺点:存储不是邻接的边也占空间,浪费

Dijkstra 算法
1.初始时，只有源点，即S = {V}。U包含除V以外的其他顶点，即U ={其余顶点}，若V与U中顶点u有边，则(U,V)值=对应边的权值，否则权值 ∞;
2.从U中选取一个离V最小的顶点k，把k加入S中;
3.若从源点V到顶点U的距离（经过顶点k）比原距离短，则更新顶点U的距离
算法缺点:不能求出两点的最短路径(Floyd算法可以)

Dijkstra 算法代码:

void Dijk(int v)//v是源点
{
  　　bool S[MAX];                                 
      int n=MAX;
  　　for(int i=1; i<=n; ++i)
 　　 {
      　　dis[i] = A[v][i];
      　　S[i] = false;                               
          path[i] = v;
   　　}
   　 dis[v] = 0; S[v] = true; 　　
 　　 for(int i=2; i<=n; i++)
 　　 {
       　　int mindist = INT;
       　　int u = v; 　　                            //找出当前未使用的点j的dist[j]最小值
      　　 for(int j=1; j<=n; ++j)
      　　    if((!S[j]) && dis[j]<mindist)
      　　    {
         　　       u = j;                            //u保存当前邻接点中距离最小的点的号码
         　 　      mindist = dis[j];
       　　   }
       　　S[u] = true;
       　　for(int j=1; j<=n; j++)
       　　    if((!S[j]) && A[u][j]<INT)
       　　    {
           　    　if(dis[u] + A[u][j] < dis[j])     //在通过新加入的u点路径找到离v点更短的路径
           　    　{
                   　　dis[j] = dis[u] + A[u][j];    //更新dist值
                   　　path[j] = u;                  //记录前驱顶点
            　　    }
        　    　}
   　　}
}

Floyd算法代码:

void Floyd(MatGraph g)
{
   int A[MAXVEX][MAXVEX];
   int path[MAXVEX][MAXVEX];
   int i,j,k;
   for(i=0;i<g.n;i++)
   {
        for(j=0;j<g.n;j++)
        {
           A[i][j]=g.edges[i][j];
           if(i!=j&&g.edges[i][j]<INF)
           {
              path[i][j]=i;   //i和j之间有1条边
           }
           else
              path[i][j]=-1;   //i和j之间没有边
        }
   }
   for(k=0;k<g.n;k++)
   {
      for(i=0;i<g.n;i++)
      {
         for(j=0;j<g.n;j++)
         {
            if(A[i][j]>A[i][k]+A[k][j])  //找到更短路径
            {
               A[i][j]=A[i][k]+A[k][j];  //修改最短路径长度
               path[i][j]=k;     //修改经过顶点k
            }
         }
      }
   }
}

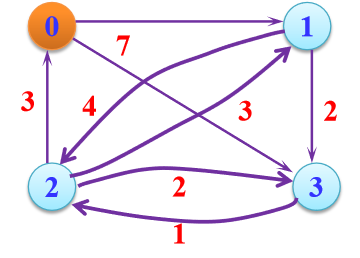
Floyd算法图示:                    

A[i][j]表示当前顶点i到顶点j的最短路径长度,path[]表示最短路径    

                                                                                                                                             A0                                                                                                      path0

    

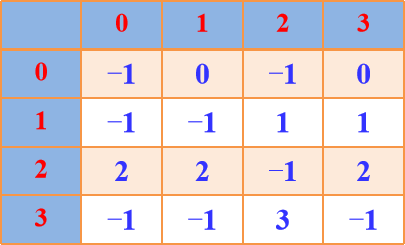
                                                                                                                                             A1                                                                                                        path1

                                                                                                 

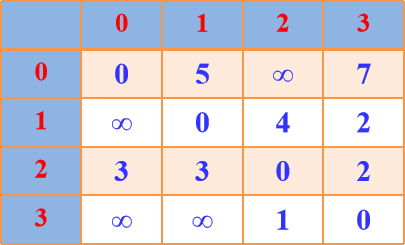
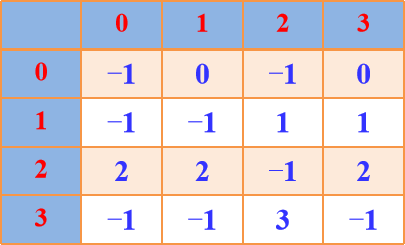
                                                                                                                                             A2                                                                                                           path2

                                                                                                 

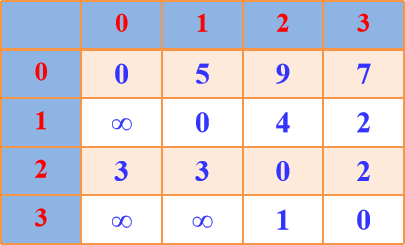
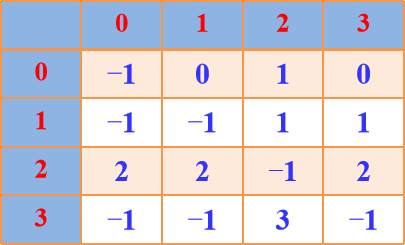
                                                                                                                                            A3                                                                                                      path3

                                                                                                   

Prim算法是多次寻找邻边的权值最小值，而Kruskal是先对权值排序后按权值递增查找，在算法效率上Kruskal比Prim快，因为Kruskal只需一次对权重的排序就能求出最小生成树,
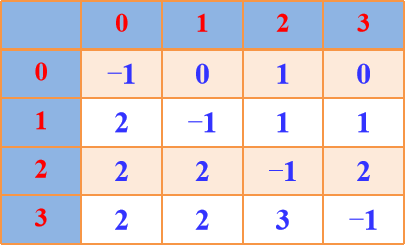
而Prim算法需要每次都对边找出权最小排序才能
Prim算法：时间复杂度O(n^2)与边数e无关、适用于稠密图和邻接矩阵存储(边的权值)
Kruskal算法：时间复杂度O(elog2e)、只与边数有关,适用于稀疏图和邻接表存储

 void Prim(MGragh G)
 {
    int min,i,j,k;//min;权值最小值
    int adjvex[MAXVEX]; //保存相关顶点下标
    int lowcost[MAXVEX];//保存相关顶点间边的权值
    lowcost[0] = 0;// 表示i那个下标的顶点加入生成树
    adjvex[0] = 0; //初始化
    for(i = 0; i < G.numVertexes; i++)//lowcost,adjevx赋初值
    {
        lowcost[i] = G.arc[v][i];
        adjvex[i] = v;
    }
    for(i = 1; i < G.numVertexes; i++) //最小生成树
    {
        min = INFITINY; //先把min置为无限大
        j = 1;
        k = 0;
        while(j < G.numVertexes)
        {
            if(lowcost[j] != 0 && lowcost[j] < min)//判断并向lowcost中添加权值
            {
                min = lowcost[j];
                k = j;//记录最近顶点的编号
            }
            j++;
        }
        printf("(%d %d)",lowcost[k],k);
        lowcost[k] = 0;//置0表示这个定点已经完成任务，找到最小权值分支
        for(j = 1; j < G.numVertexes; j++)
        {
            if(lowcost[j] != 0 && G.arc[k][j] < lowcost[j])
            {
                lowcost[j] = G.arc[k][j];
                adjvex[j] = k;//修改数组lowcost,adjvex
            }
        }
    }
}

拓扑排序是将一个有向无环图G=(V,E)的所有顶点排成一个线性序列，使得有向图中的任意的顶点u 和v构成的边或弧,(u,v)属于该图的边集,并且使得u始终是出现在v前面
前提:有向无环图;目的:表示活动的优先/先后关系
算法思想：1.找到有向无环图中没有前驱的顶点,输出;2.从图中删除此节点且删除该节点发出的所有边或弧

关键路径：从有向图的源点到汇点的最长路径

关键路径的长度:完成这项活动的最短时间

事件的最早开始时间：事件v的最早开始事件，一定是所有前驱事件x，y，z完成，才轮到事件v

ve(v)=max{ve(x)+a,ve(y)+b,ve(z)+c}

事件的最迟开始时间：保证后继所有事件能按时完成的最小值

vl(v）=min{vl(x)-a,vl(y)-b,vl(z)-c}

3.疑难问题及解决方案(如果有的话，不求多但求精。可包含编程题，可只包含无解决方案的疑难问题)

1.输出无向图中从顶点u→v的所有简单路径(深度优先遍历),用队列法

2.图着色问题(伪代码)

CreateMGraph建邻接矩阵
初始化图
    输入n;
    for(i=0to n)
    {
    flag,num为0;
    color数组为0;
    for(j=0 to n）{
    输入color[j];
    if(该颜色没出现过){
    该颜色置为1;
    num++;
    }
    if(flag为0同时颜色数量没有超出限制){
    for(遍历标号比他小的所有连通的点)
    if(相邻顶点颜色重合)
    flag=1;
    }
    if(出现相同颜色或者颜色过多)输出No；
    否则输出Yes;
    }