代码:
import java.util.*; import java.util.Scanner; /* *动态规划思想解决0/1背包问题 */ public class LeetCode{ public static void main(String[] args){ Scanner in=new Scanner(System.in); System.out.println("输入背包的容量"); int bagCap=in.nextInt(); //背包的容量 System.out.println("总共有多少个物品"); int n=in.nextInt(); //总共有多少个物品 int[][] mono=new int[2][n]; // 2行n列,第一行表示物品的重量,第二行表示物品的价值 int[][] dp=new int[n][bagCap+1]; //表,数组下标从0开始,加1防止数组溢出 System.out.println("依次输入物品的重量和价值"); for(int i= 0;i<n;i++){ mono[0][i]=in.nextInt(); mono[1][i]=in.nextInt(); } //初始化最小子问题的最优解,即考虑物品n的最优解情形 for(int j=0;j<=bagCap;j++){ if(j>=mono[0][n-1]){ dp[n-1][j]=mono[1][n-1]; }else{ dp[n-1][j]=0; } } //自低向上打表,要始终记住数学符号的含义:dp[i][j] 表示可选物品是i,i+1,.......,n,背包容量是j时问题的最优解 for(int i=n-2;i>=0;i--){ for(int j=0;j<=bagCap;j++){ if(j>=mono[0][i]){ dp[i][j]=Math.max(dp[i+1][j],dp[i+1][j-mono[0][i]]+mono[1][i]); }else{ dp[i][j]=dp[i+1][j]; } } } System.out.println("最优解是:"+dp[0][bagCap]); } }
测试:
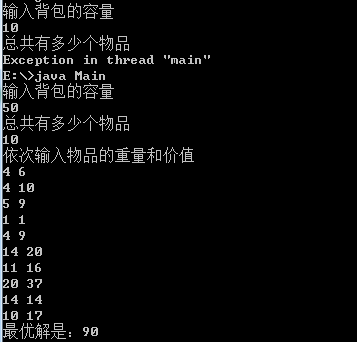
0/1 背包问题可以扩展变形到其他问题,举个栗子:

两个cpu,如果其中一个分摊的时间越接近sum/2那么总的处理时间便越小,转换成0/1背包问题,n个任务,一个容量为sum/2的袋子(cpu),求这个袋子能装的最大重量。这题我在做的时候,有两种动态规划的解法:
从物品重量到sum/2计算:
public class Main{
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int[] tasks=new int[n];
int sum=0;
for(int i=0;i<n;i++){
tasks[i]=sc.nextInt()>>10;
sum=sum+tasks[i];
}
int dp[]=new int[sum/2+1];
for(int task:tasks){
for(int i=task;i<=sum/2;i++){
dp[i]=Math.max(dp[i],dp[i-task]+task);
}
}
System.out.println(Math.max(dp[sum/2],sum-dp[sum/2])<<10);
}
}
和从sum/2到物品重量计算:
public class Main{
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int[] tasks=new int[n];
int sum=0;
for(int i=0;i<n;i++){
tasks[i]=sc.nextInt()>>10;
sum=sum+tasks[i];
}
int dp[]=new int[sum/2+1];
for(int task:tasks){
for(int i=sum/2;i>=task;i--){
dp[i]=Math.max(dp[i],dp[i-task]+task);
}
}
System.out.println(Math.max(dp[sum/2],sum-dp[sum/2])<<10);
}
}
第一种和第二中的区别仅仅在于计算每个物品放入或不放的最优解时计算过程一个是从物品重量遍历到袋子容量,另一种是从袋子容量遍历到物品重量。然而第一种解法只通过了80%的测试案例,而第二种却能完全通过。原因在于第一种会出现重复放入同一物品的情况:
假设判断到了第3个物品,重量是10,袋子的容量是100,那么便从dp[10]开始计算最优解,一直到dp[20],这其中的最优解中第3个物品可能是放入的也可能是不放入的,当我门计算到dp[21]时,会计算到dp[11]+10,这个时候会利用到最优解dp[11],但是dp[11]的最优解很可能是已经将第3个物品放入了,因此出现了重复放入同一物品的情况,导致结果出错。而从从袋子容量遍历到物品重量则不会出现这个问题,当从dp[100]遍历到dp[10]的时候,因为是从大到小计算的,如果要用到较小的dp[11],这个时候的dp[11]还是上一物品(物品2)遍历计算得到的结果,因此不会出现重复放入同一物品的情况。