Problem 2

题目

Each new term in the Fibonacci sequence is generated by adding the previous two terms. By starting with 1 and 2, the first 10 terms will be:

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms.

提醒：even-valued 是偶数的意思，英文不好的同学表示：-_-|||

最简单的解答

public static long q2(int max) {
            long s1 = 1;
            long s2 = 2;

            long sum = 2;
            while (s2 <= max) {
                s1 = s1 + s2;//(s3)
                s2 = s1 + s2;//(s4 = s3 + s2)
                if (s1 <= max && s1 % 2 == 0) {
                    sum += s1;
                }
                if (s2 <= max && s2 % 2 == 0) {
                    sum += s2;
                }
            }
            return sum;
        }

        public static void test() {
            var t1 = DateTime.Now;
            Console.WriteLine(" " + q2(4000000) + " cast time " + (DateTime.Now - t1).TotalSeconds);

        }

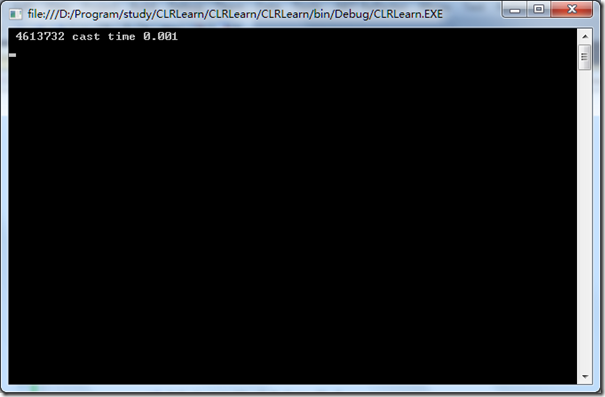
运行结果

当然还有很多可以简化复杂的方法。

第一点：比如对%2，如果c#运行的时候，没有对其特别优化（判断最后一位是否是0），则可以考虑使用规律来减少判断。规律是：

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

S1奇数，S2偶数，S3奇=奇+偶，S4奇数=奇数+偶数，S5=偶数。。。

也就是说，从2开始，每隔2个就是一个偶数。

甚至可以得出一个偶数的递推公式。

O1=S2=2;

O2=S5=S3+S4;

O3=S8=S6+S7;

.......

O2=O1+1   +   O1=O1*2+1=。。。

O3=O2+S4+O2

....

好吧。。最终可以得出一个通项公式；

参考这里 http://www.cnblogs.com/zhouyinhui/archive/2011/01/06/1929153.html

挖个坑。有时间再填满中间漏掉的推理。