5中排序算法（冒泡，选择，插入，快速，归并）

1冒泡排序

比较相邻的元素，将小的放到前面,(每一轮找出数组中最大的放在后面，后面排好序的数组元素不参与下轮排序)。

下面将数组[7,8,5,1,3]里面的元素进行排序。

7 8 5 1 3

1.1:   7 8 5 1 3     7和8进行比较，因为7<8所以2个元素的位置不变
1.2:   5 7 1 3 8     8和5进行比较，因为8>5所以2个元素的位置互换
1.3:   7 5 1 8 3     8和1进行比较，因为8>1所以2个元素的位置互换
1.4:   7 5 1 3 8     同理，8和3互换位置，得到最大数8，并且不参与下一轮排序
2.1:   5 7 1 3 8     同理第二轮排序得到最大数是7，放在最后，依次得到每一轮的最大值，这样小的数就在前面，大
的数放在后面，最后得到所要的数组[1,3,5,7,8]。

/**
     * @Description 比较相邻的元素，将小的放到前面,(每一轮找出数
     * 组中最大的放在后面，后面排好序的数组元素不参与下轮排序)
     * @MethodName bubbingSort  
     * @Date 14:51 2019/5/27
     * @Param [arr]
     * @Return void
     * @Throws
     */
    public static void bubbingSort(int[] arr) {
        //外层循环控制排序趟数
        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = 0; j < arr.length - 1 - i; j++) {
                //内层循环控制每一趟排序多少次
                if (arr[j] < arr[j + 1]) {
                    int temp = arr[j + 1];
                    arr[j + 1] = arr[j];
                    arr[j] = temp;
                }
                System.out.println("bubbingSort " + i + Arrays.toString(arr));
            }
        }
    }

 

2选择排序

1.将数组中每个元素与第一个元素比较，如果这个元素小于第一个元素，则交换这两个元素

2.循环第1条规则，找出最小元素，放于第1个位置

3.经过n-1轮比较完成排序

/**
     * @Description 1.将数组中每个元素与第一个元素比较，如果这个元素小
     * 于第一个元素，则交换这两个元素
     * 2.循环第1条规则，找出最小元素，放于第1个位置
     * 3.经过n-1轮比较完成排序
     * @MethodName selectSort
     * @Date 14:48 2019/5/27
     * @Param [arr]
     * @Return void
     * @Throws
     */
    public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            int value = arr[i];
            int position = i;
            //内层循环查找最小数，并记录最小数的位置
            for (int j = i + 1; j < arr.length; j++) {
                //获取到最小数之后每次都用最小数于之后的数进行比较
                if (arr[j] < value) {
                    value = arr[j];
                    position = j;
                }
            }
            //内层循环结束交换
            arr[position] = arr[i];
            arr[i] = value;
            System.out.println("selectSort " + i + Arrays.toString(arr));
        }

    }

 

3插入排序

1.将数组分为两部分, 将后部分的第一个逐一与前部分每一个元素比较，在合理位置插入

2.插入排序算法效率要高于选择排序和冒泡排序 

 

7 8 5 1 3 将数组分为7和8,5,1,3两部分

1: 7   8 5 1 3 8>7，所以位置不变

2: 5   7 8 1 3 5<8 && 5<7,所以5放到7和8的前面 

3: 1   5 7 8 3 1< 8 && 1<7 && 1<5,所以1放到5,7,8的前面

4: 1   3 5 7 8 将3依次和前面元素比较，得到3<5,1>3，所以3在1和5之间，结束 

/**
     * @Description 1.将数组分为两部分, 将后部分的第一个逐一与前部分每
     * 一个元素比较，在合理位置插入    Arrays.sort(); 快排
     * 2.插入排序算法效率要高于选择排序和冒泡排序
     * @MethodName insertSort
     * @Date 14:54 2019/5/27
     * @Param [arr]
     * @Return void
     * @Throws
     */
    public static void insertSort(int[] arr) {
        int insertNum;
        for (int i = 1; i < arr.length; i++) {
            //从第一个数开始执行插入
            insertNum = arr[i];
            int j = i - 1;
            //将大于insertNum 向后移动（等于交换位置）
            while (j >= 0 && arr[j] > insertNum) {
                arr[j + 1] = arr[j];
                j--;
            }
            arr[j + 1] = insertNum;
            System.out.println("insertSort " + i + Arrays.toString(arr));
        }

    }

4快速排序

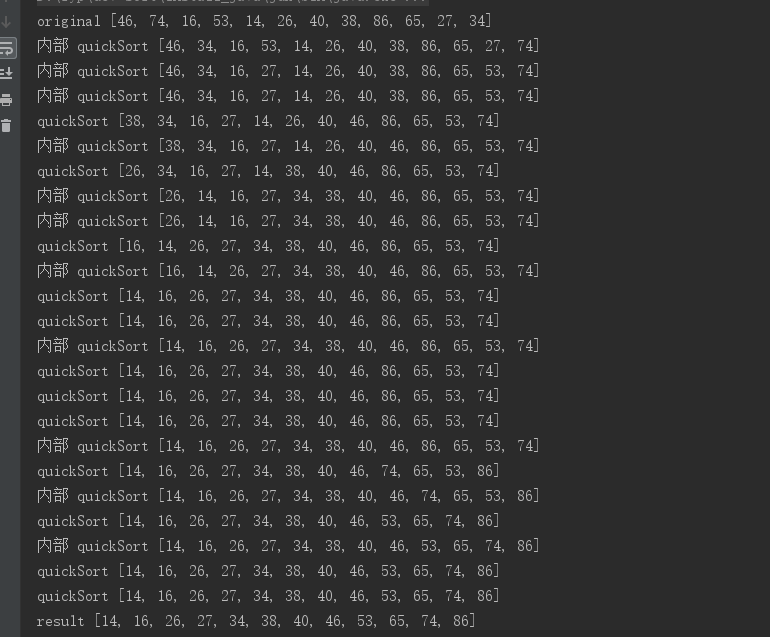
通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

10 4 7 8 5 9 3 12 11

1: 选10位一个基准数，进行第一次排序，小于10的放左边，大于10的放右边，得到新的数组[4,7,8,5,9,3,10,12,11],以10为基准分成左右2部分,[4,7,8,5,9, 3],10,[12,11]，两边数组分别进行快速排序,以数组第一个元素作为基准进行排序。

当前数据为[4,7,8,5,9,3],10,[12,11]

2: [4,7,8,5,9,3]以第一个元素4作为基准排序得到[3,4,5,7,8,9]；后面的数组为[11,12]，结束。

当前数据为[3],4,[5,7,8,9],10,11,12，因为3为单个的，所以[3]不需再进行排序，目前只需对[5,7,8,9]进行处理

3: [5,7,8,9],以第一个元素5作为基准排序，得到5,[,7,8,9]当前数据为3,4,5,[7,8,9],10,11,12

4: 类似步骤3，分别把7,8,9给独立出来，最终得到数据3,4,5,7,8,9,10,11,12

 /**
     * @Description 选择一个基数，小于基数的在左边，大于基数在右边 通过一趟排序将要排序的数据分割成独立的两部分，其中
     * 一部分的所有数据都比另外一部分的所有数据都要小，然后再按
     * 此方法对这两部分数据分别进行快速排序，整个排序过程可以递
     * 归进行，以此达到整个数据变成有序序列
     * @MethodName quickSort
     * @Date 16:10 2019/5/27
     * @Param [a]
     * @Return void
     * @Throws
     */
    public static void quickSort(int[] arr, int low, int high) {
        int i, j, temp, t;
        if (low > high) {
            return;
        }
        i = low;
        j = high;
        //temp就是基准位
        temp = arr[low];
        while (i < j) {
            //先看右边，依次往左递减
            //{5, 2, 7, 3, 8};
            //5<8 y-1 5《3 不成立 y=3（从右开始找比基数小的位置）
            while (temp <= arr[j] && i < j) {
                j--;
            }
            //再看左边，依次往右递增
            //{5, 2, 7, 3, 8}; 5>2 i++ i=2 5>7 i=2(从左开始找比基数大的位置）
            while (temp >= arr[i] && i < j) {
                i++;
            }
            //如果满足条件则交换 
            if (i < j) {
                t = arr[j];
                arr[j] = arr[i];
                arr[i] = t;
            }

        }
        //最后将基准为与i和j相等位置的数字交换
        arr[low] = arr[i];
        arr[i] = temp;
        System.out.println("quickSort " + Arrays.toString(arr));
        //递归调用左半数组
        quickSort(arr, low, j - 1);
        //递归调用右半数组
        quickSort(arr, j + 1, high);

    }

5归并排序

该算法是采用分治法（DIVIDE AND CONQUER）的一个非常典型的应用，且各层分治递归可以同时进行

/**
     * @Description 分而治之(divide - conquer);每个递归过程涉及三个步骤
     * 第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.
     * 第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作
     * 第三, 合并: 合并两个排好序的子序列,生成排序结果.
     * @MethodName mergeSort
     * @Date 17:23 2019/5/27
     * @Param [a, low, high]
     * @Return int[]
     * @Throws
     */
    public static int[] mergeSort(int[] a, int low, int high) {
        int mid = (low + high) / 2;
        if (low < high) {
            mergeSort(a, low, mid);
            mergeSort(a, mid + 1, high);
            //左右归并
            merge(a, low, mid, high);
        }
        return a;
    }

    public static void merge(int[] a, int low, int mid, int high) {
        int[] temp = new int[high - low + 1];
        int i = low;
        int j = mid + 1;
        int k = 0;
        // 把较小的数先移到新数组中
        while (i <= mid && j <= high) {
            if (a[i] < a[j]) {
                temp[k++] = a[i++];
            } else {
                temp[k++] = a[j++];
            }
        }
        // 把左边剩余的数移入数组
        while (i <= mid) {
            temp[k++] = a[i++];
        }
        // 把右边边剩余的数移入数组
        while (j <= high) {
            temp[k++] = a[j++];
        }
        // 把新数组中的数覆盖nums数组
        for (int x = 0; x < temp.length; x++) {
            a[x + low] = temp[x];
        }
    }