LeetCode 120. Triangle 20170706 部分之前做了没写的题目

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.

题目大意：

给定一个三角形，找出从顶到底的路径的最小和。每一步只能走到相邻的结点

解题思路：

应该是用动态规划的方法。用一个数组array来保存三角形每一行从顶点到该行的点的最小距离。每一次更新当前行的数值前，array保存的实际上是上一行的数值。在更新的过程中直接利用上一行的数值来继续更新，由于每个点都跟上一行的两个点相邻，所以每个点的顶点到该点的最小值实际上是由跟他相邻的两个点的中的最小值加上该点的值。需要注意的是最左边的点和最右边的点由于只有一个上一行的点相邻，所以不需要比较最小值，直接从上个点的数值加上当前数值。值得注意的一点是为了不影响array数组的值，所以每次每一行的更新都从右边开始更新。到了最后一行的时候，只要返回其中的最小值即可。

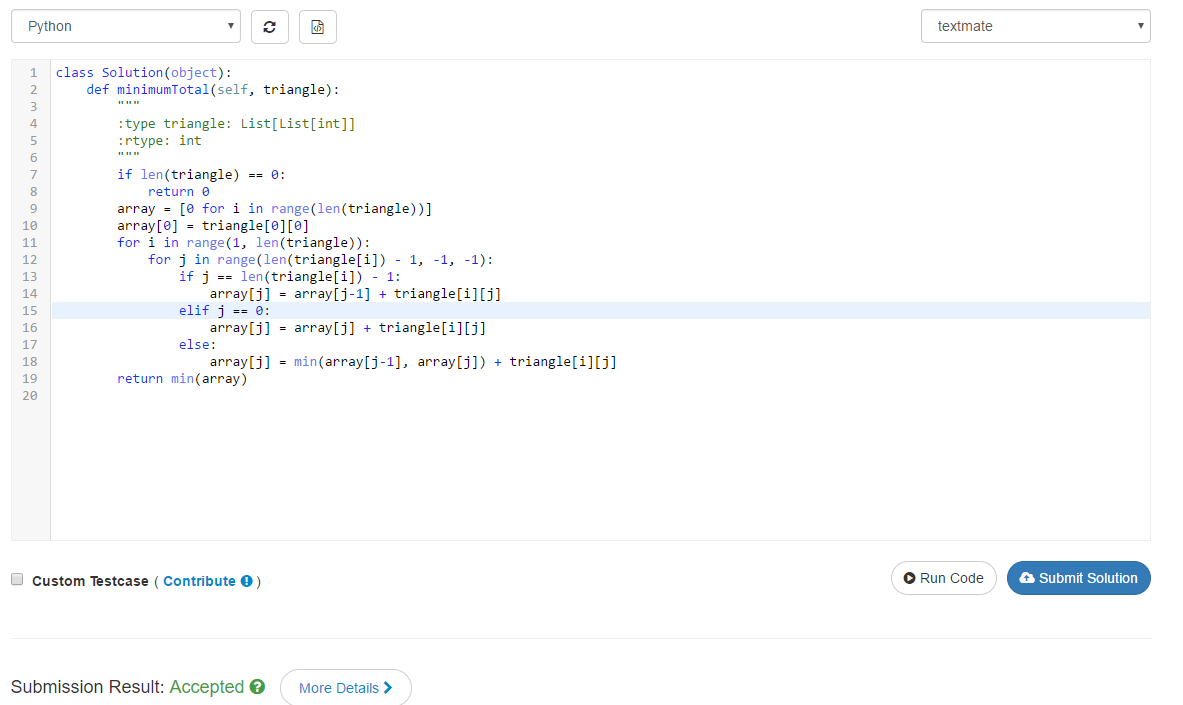
class Solution(object):
　　def minimumTotal(self, triangle):
　　　　"""
　　　　:type triangle: List[List[int]]
　　　　:rtype: int
　　　　"""
　　　　if len(triangle) == 0:
　　　　　　return 0
　　　　array = [0 for i in range(len(triangle))]
　　　　array[0] = triangle[0][0]
　　　　for i in range(1, len(triangle)):
　　　　　　for j in range(len(triangle[i]) - 1, -1, -1):
　　　　　　　　if j == len(triangle[i]) - 1:
　　　　　　　　　　array[j] = array[j-1] + triangle[i][j]
　　　　　　　　elif j == 0:
　　　　　　　　　　array[j] = array[j] + triangle[i][j]
　　　　　　　　else:
　　　　　　　　　　array[j] = min(array[j-1], array[j]) + triangle[i][j]
　　　　return min(array)