题目:给定一个图的邻接矩阵,求出该图的所有最大团。(最大完全子图)

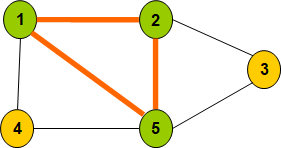
1.自己思考的朴素算法
(1)根据题意画出解空间树(只以以1结点开始为例,其余以其他结点开始的同下述方法)(下图中绿色结点为进入递归,红色结点为不进入递归)
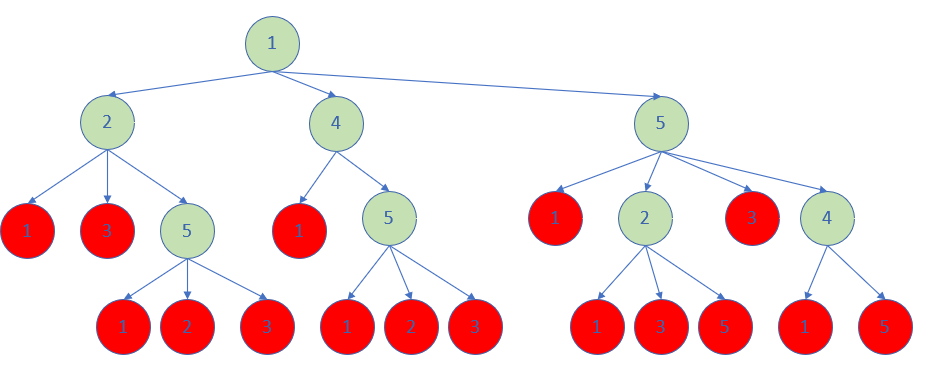
从图中发现,一种想法是按深度遍历解集。关键问题就是如何设置递归的出口和去重。
(2)算法思路。
【1】设置一最大团列表。其中的每一个元素即是一个最大团。并记录最大团的长度。
【2】设置一个临时最大团列表。
对每一个结点深度优先搜索(这里以1为例)。
【1】将1加入临时最大团列表。
对与1相连的所有结点进行判断,如果该结点和临时最大团的所有结点都相连(邻接矩阵的定义格式使得该结点在临时最大团中的去重工作,在相连判断中已经做完)
那么对该点进行递归调用。这里进入2结点的递归。
【2】将2加入临时最大团列表。
对2的所有相连结点进行判断,1和1无相连边(重复),3和1无相连边,5和1有相连边。这里进入结点5的递归
【3】将5加入临时最大团列表。
对5的所有相连结点进行判断,1和1无相连边(重复),2和2无相连边(重复),3和1无相连边。
退出递归,返回最上层。开始进入结点4的递归........
由此我们可以找到所有完全子图。下面讨论设置递归的出口。即每次深度遍历到最后时,把临时最大团加入到最大团列表的时机。
算法行进到某一结点时,如果在该结点不递归操作。那么这就是递归结束的时候,但这并不意味着从某一结点开始的递归遍历,已经到达最深处。
在此可以进行判断,比较当前临时最大团的长度和最大团列表的长度。
如果当前临时最大团的长度大于最大团列表的长度,那么意味着当前找到的完全子图要比之前找到的完全子图大。
则清空原先的最大图列表,将新找到的临时最大子图加入,并重置临时最大团长度。
如果当前临时最大团的长度等于最大团列表的长度,那么意味着当前找到的完全子图应该被加入到最大团列表。
这时又出现了新的问题,即当前新找到的临时完全最大团是否会和最大团列表中的某一团重复?为了解决去重问题,我将
最大团列表中的每一个最大团和临时最大团进行比较。比较的方法时,将两者都先进行排序(元素位置可能不同不利于判断),排序后顺次比较对应元素,
如果临时最大团的元素和最大团列表中的所有最大团的元素都不相同,则将该临时最大团加入到最大团列表。
如果当前临时最大团的长度小于最大团列表的长度,则说明递归没有进行到最深处或该完全子图不是最大完全子图,不处理即可。
(3)算法完整代码
# include <iostream> # include <vector>
using namespace std; void maxTuan(int eages[][25], int n, int index, vector<int> *tempLump); void sort(vector<int> *lump);
vector<vector<int>> maxlumps; int maxLength = 0; int main() { int n; int eages[25][25]; cin >> n; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { cin >> eages[i][j]; } } for (int i = 0; i < n; i++) { vector<int> lump; maxTuan(eages, n, i, &lump); } for (int i = 0; i < maxlumps.size(); i++) { for (int j = 0; j < maxlumps.at(i).size(); j++) { cout << maxlumps.at(i).at(j) << "\t"; } cout << endl; } return 0; } /* 名称:最大团算法 功能:从一个结点开始,寻找其最大完全子图 */ void maxTuan(int eages[][25],int n,int index,vector<int> *tempLump) { tempLump->push_back(index); for (int i = 0; i < n; i++) { if (eages[index][i] == 1) { bool inlump = true; for (int j = 0; j < tempLump->size(); j++) { if (eages[i][tempLump->at(j)] == 0) { inlump = false; break; } } if (inlump) { vector<int> newTempLump; newTempLump.insert(newTempLump.end(),tempLump->begin(),tempLump->end()); //这里注意每次递归时赋予一个新的临时最大团列表,避免使用同一个列表造成数据错误 maxTuan(eages,n,i, &newTempLump); } else { if (tempLump->size() > maxLength) { maxLength = tempLump->size(); maxlumps.clear(); maxlumps.push_back(*tempLump); } else if (tempLump->size() == maxLength) { bool pushMark = false; for (int k = 0; k < maxlumps.size(); k++) { sort(&maxlumps.at(k)); sort(tempLump); int count = 0; for (int o = 0; o < maxLength; o++) { if (maxlumps.at(k).at(o) == tempLump->at(o)) { count++; } } if (count != 3) { pushMark = true; } else { pushMark = false; break; } } if (pushMark) { maxlumps.push_back(*tempLump); } } } } } } /* 冒泡排序法 */ void sort(vector<int> *lump) { for (int i = 0; i < lump->size() - 1; i++) { for (int j = 0; j < lump->size() - 1; j++) { if (lump->at(j) > lump->at(j + 1)) { int change = lump->at(j); lump->at(j) = lump->at(j + 1); lump->at(j + 1) = change; } } } }