sklearn LDA降维算法
LDA(Linear Discriminant Analysis)线性判断别分析,可以用于降维和分类。其基本思想是类内散度尽可能小,类间散度尽可能大,是一种经典的监督式降维/分类技术。
sklearn代码实现
#coding=utf-8
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import numpy as np
def main():
iris = datasets.load_iris() #典型分类数据模型
#这里我们数据统一用pandas处理
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data['class'] = iris.target
#这里只取两类
# data = data[data['class']!=2]
#为了可视化方便,这里取两个属性为例
X = data[data.columns.drop('class')]
Y = data['class']
#划分数据集
X_train, X_test, Y_train, Y_test =train_test_split(X, Y)
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X_train, Y_train)
#显示训练结果
print lda.means_ #中心点
print lda.score(X_test, Y_test) #score是指分类的正确率
print lda.scalings_ #score是指分类的正确率
X_2d = lda.transform(X) #现在已经降到二维X_2d=np.dot(X-lda.xbar_,lda.scalings_)
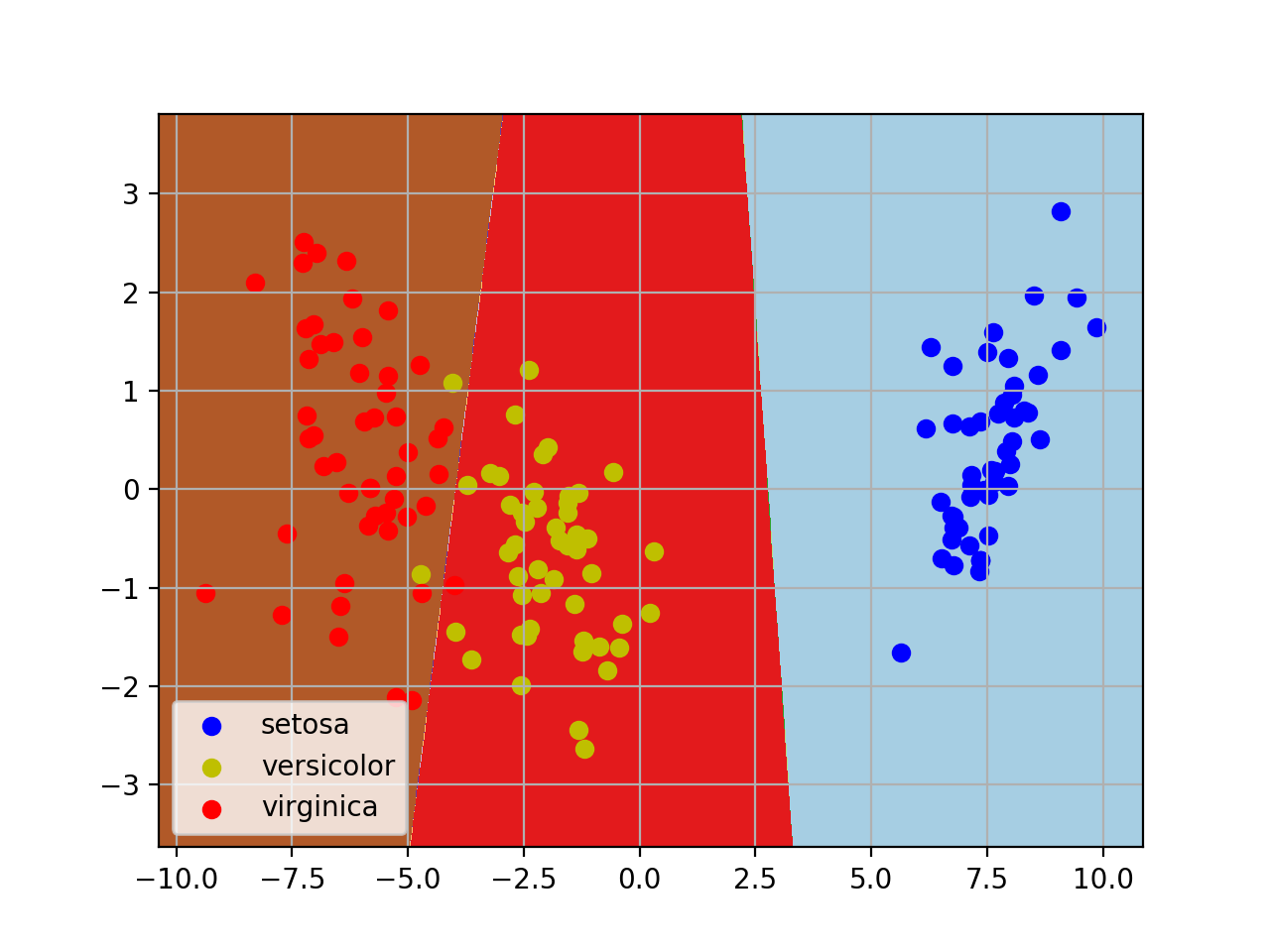
#对于二维数据,我们做个可视化
#区域划分
lda.fit(X_2d,Y)
h = 0.02
x_min, x_max = X_2d[:, 0].min() - 1, X_2d[:, 0].max() + 1
y_min, y_max = X_2d[:, 1].min() - 1, X_2d[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = lda.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
#做出原来的散点图
class1_x = X_2d[Y==0,0]
class1_y = X_2d[Y==0,1]
l1 = plt.scatter(class1_x,class1_y,color='b',label=iris.target_names[0])
class1_x = X_2d[Y==1,0]
class1_y = X_2d[Y==1,1]
l2 = plt.scatter(class1_x,class1_y,color='y',label=iris.target_names[1])
class1_x = X_2d[Y==2,0]
class1_y = X_2d[Y==2,1]
l3 = plt.scatter(class1_x,class1_y,color='r',label=iris.target_names[2])
plt.legend(handles = [l1, l2, l3], loc = 'best')
plt.grid(True)
plt.show()
if __name__ == '__main__':
main()
测试结果
Means: #各类的中心点
[[ 5.00810811 3.41891892 1.44594595 0.23513514]
[ 6.06410256 2.80769231 4.32564103 1.33589744]
[ 6.61666667 2.97222222 5.63055556 2.02777778]]
Score: #对于测试集的正确率
0.973684210526
Scalings:
[[ 1.19870893 0.76465114]
[ 1.20339741 -2.46937995]
[-2.55937543 0.42562073]
[-2.77824826 -2.4470865 ]]
Xbar:
[ 5.89285714 3.0625 3.79375 1.19464286]
#X'=np.dot(X-lda.xbar_,lda.scalings_)默认的线性变化方程