前缀和

前缀和技巧

问题引入--获取数组中任意区间段的和

描述

比如说给你一个数组 nums，让你实现一个接口 sum(i, j)，这个接口要返回 nums[i..j] 的和，而且会被多次调用，你怎么实现这个接口呢？

因为接口要被多次调用，显然不能每次都去遍历 nums[i..j]，有没有一种快速的方法在 O(1) 时间内算出 nums[i..j] 呢？这就需要前缀和技巧了。

解析

对于一个给定的数组 nums，我们额外开辟一个前缀和数组进行预处理：

int n = nums.length;
// 前缀和数组
int[] preSum = new int[n + 1];
preSum[0] = 0;
for (int i = 0; i < n; i++)
    preSum[i + 1] = preSum[i] + nums[i];

//nums[i...j] = preSum[j+1] - preSum[i]

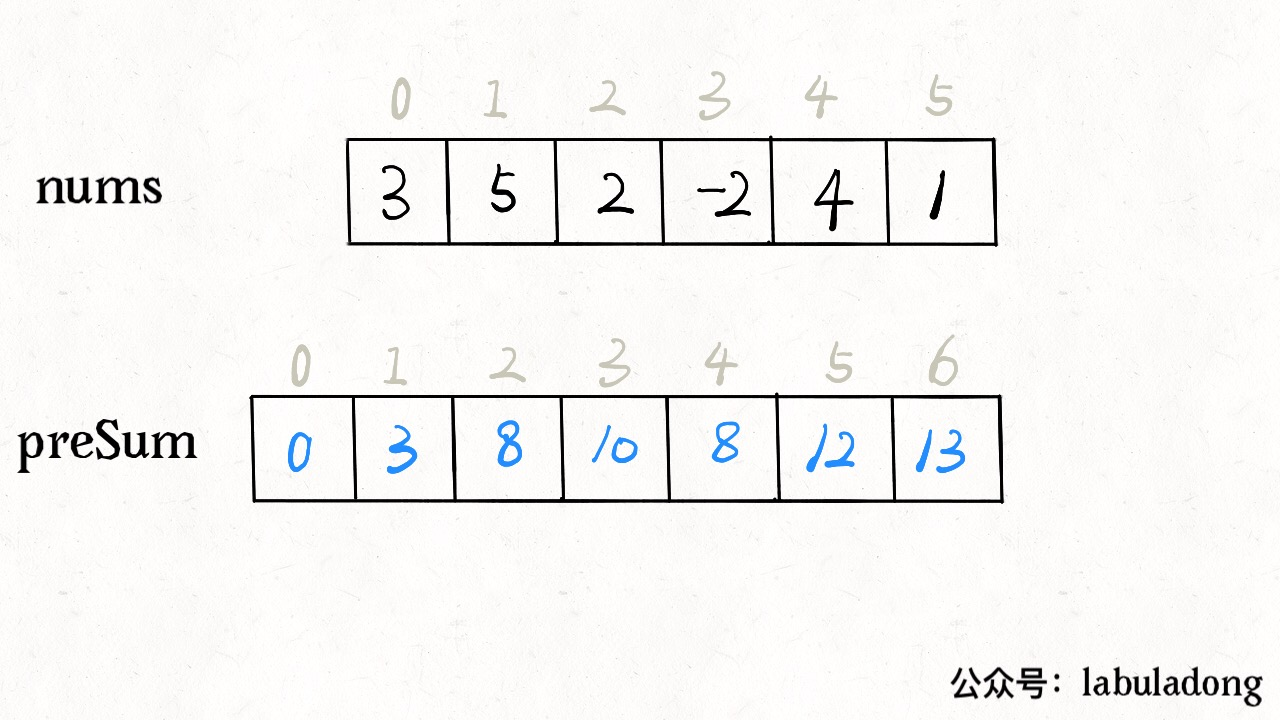
 这个前缀和数组 preSum 的含义也很好理解，preSum[i] 就是 nums[0..i-1] 的和。那么如果我们想求 nums[i..j] 的和，只需要一步操作 preSum[j+1]-preSum[i] 即可，而不需要重新去遍历数组了。

问题--数组中和为k的连续子数组的个数

描述

给定一个整数数组和一个整数k，你需要找到该数组中和为k的连续子数组的个数。

例如：输入：nums=[1,1,1]，k=2    输出：2，[1,1][1,1]为2种不同情况。

直接代码

根据上面的例题，可以得出：

int subarraySum(int[] nums, int k) {
    int n = nums.length;
    // 构造前缀和
    int[] sum = new int[n + 1];
    sum[0] = 0; 
    for (int i = 0; i < n; i++)
        sum[i + 1] = sum[i] + nums[i];
    
    int ans = 0;
    // 穷举所有子数组
    for (int i = 1; i <= n; i++)
        for (int j = 0; j < i; j++)
            // sum of nums[j..i-1]
            if (sum[i] - sum[j] == k)
                ans++;

    return ans;
}

这个解法的时间复杂度 O(N^2) 空间复杂度 O(N)，并不是最优的解法。不过通过这个解法理解了前缀和数组的工作原理之后，可以使用一些巧妙的办法把时间复杂度进一步降低。

优化代码

优化的思路是：我直接记录下有几个 sum[j] 和 sum[i] - k 相等，直接更新结果，就避免了内层的 for 循环。我们可以用哈希表，在记录前缀和的同时记录该前缀和出现的次数。

将复杂度降低到O(N)

int subarraySum(int[] nums, int k) {
    int n = nums.length;
    // map：前缀和 -> 该前缀和出现的次数
    HashMap<Integer, Integer> preSum = new HashMap<>();
    // base case
    preSum.put(0, 1);

    int ans = 0, sum0_i = 0;
    for (int i = 0; i < n; i++) {
        sum0_i += nums[i];
        // 这是我们想找的前缀和 nums[0..j]
        int sum0_j = sum0_i - k;
        // 如果前面有这个前缀和，则直接更新答案
        if (preSum.containsKey(sum0_j))
            ans += preSum.get(sum0_j);

        // 把前缀和 nums[0..i] 加入并记录出现次数
        preSum.put(sum0_i, preSum.getOrDefault(sum0_i, 0) + 1);
    }
    return ans;
}