BST 二叉搜索树源码笔记

tree.h

typedef int ElementType;

/* START: fig4_16.txt */
#ifndef _Tree_H
#define _Tree_H

struct TreeNode; // 定义结构体节点
typedef struct TreeNode *Position; // 指向节点的指针
typedef struct TreeNode *SearchTree; // 指针，表示搜索树，是搜索树的根节点

SearchTree MakeEmpty( SearchTree T );
Position Find( ElementType X, SearchTree T );
Position FindMin( SearchTree T );
Position FindMax( SearchTree T );
SearchTree Insert( ElementType X, SearchTree T );
SearchTree Delete( ElementType X, SearchTree T );
ElementType Retrieve( Position P );

#endif  /* _Tree_H */

/* END */

tree.c

#include "tree.h"
#include <stdlib.h>
#include "fatal.h"

struct TreeNode
{
    ElementType Element; // 树节点存储的元素
    SearchTree Left; // 左子树
    SearchTree Right; // 右子树
};

/* START: fig4_17.txt */
// 建立一棵空树
SearchTree
MakeEmpty(SearchTree T)
{
    if (T != NULL)
    {
        MakeEmpty(T->Left); // 递归删除左子树
        MakeEmpty(T->Right); // 递归删除右子树
        free(T); // 释放该节点
    }
    return NULL;
}
/* END */

/* START: fig4_18.txt */
// 二叉搜索树的查找操作
Position
Find(ElementType X, SearchTree T)
{
    if (T == NULL)
        return NULL;
    if (X < T->Element) // 如果待查找元素比根节点小，那么递归查找左子树
        return Find(X, T->Left);
    else if (X > T->Element) // 如果待查找元素比根节点大，那么递归查找右子树
        return Find(X, T->Right);
    else
        return T;
}
/* END */

/* START: fig4_19.txt */
// 查找最小元素，即找出最左边的叶子节点
Position
FindMin(SearchTree T)
{
    if (T == NULL)
        return NULL;
    else if (T->Left == NULL)
        return T;
    else
        return FindMin(T->Left);
}
/* END */

/* START: fig4_20.txt */
// 查找最大值
Position
FindMax(SearchTree T)
{
    if (T != NULL)
        while (T->Right != NULL)
            T = T->Right;

    return T;
}
/* END */

/* START: fig4_22.txt */
// 插入操作
SearchTree
Insert(ElementType X, SearchTree T)
{
/* 1*/      if (T == NULL)
            {
        /* Create and return a one-node tree 创建并返回一个单节点树 */
/* 2*/          T = malloc(sizeof(struct TreeNode));
/* 3*/          if (T == NULL)
/* 4*/              FatalError("Out of space!!!"); // 空间用尽的情况
                else
                {
/* 5*/              T->Element = X; // 赋值
/* 6*/              T->Left = T->Right = NULL; // 左右子树置空
                }
            } else
/* 7*/      if (X < T->Element)
/* 8*/          T->Left = Insert(X, T->Left); // 递归寻找合适的插入位置
            else
/* 9*/      if (X > T->Element)
/*10*/          T->Right = Insert(X, T->Right);
            /* Else X is in the tree already; we'll do nothing */

/*11*/      return T;  /* Do not forget this line!! */
}
/* END */

/* START: fig4_25.txt */
// 删除操作
SearchTree
Delete(ElementType X, SearchTree T)
{
    Position TmpCell;

    // 寻找节点
    if (T == NULL)
        Error("Element not found");
    else if (X < T->Element)  /* Go left */
        T->Left = Delete(X, T->Left);
    else if (X > T->Element)  /* Go right */
        T->Right = Delete(X, T->Right);
    else  /* Found element to be deleted 找到了该删除的节点 */
    {
        if (T->Left && T->Right)  /* Two children 有两个孩子 */
        {
            /* Replace with smallest in right subtree 用右子树中最小的节点进行替换 */
            TmpCell = FindMin(T->Right); // 找出右子树中最小的节点
            T->Element = TmpCell->Element; // 替换
            T->Right = Delete(T->Element, T->Right); // 删除刚刚的那个在右子树中最小的节点
        } else  /* One or zero children 有 1 个或者 0 个孩子 */
        {
            TmpCell = T;
            if (T->Left == NULL) /* Also handles 0 children */
                T = T->Right; // 如果左子树为空，那么将 T 更新为右子树，下同
            else if (T->Right == NULL)
                T = T->Left;
            free(TmpCell); // 释放原来的 T 节点
        }
    }


    return T;
}

/* END */

// 取出 Position P 中的元素
ElementType
Retrieve(Position P)
{
    return P->Element;
}

main.c(testtree.c，测试函数)

#include "tree.h"
#include <stdio.h>

int main( )
{
    SearchTree T;
    Position P;
    int i;
    int j = 0;

    T = MakeEmpty( NULL ); // 创建一棵空树
    for( i = 0; i < 50; i++, j = ( j + 7 ) % 50 ) // 将 50 个数插入树中
        T = Insert( j, T );
    for( i = 0; i < 50; i++ )
        if( ( P = Find( i, T ) ) == NULL || Retrieve( P ) != i ) // 测试查找函数
            printf( "Error at %d
", i );

    for( i = 0; i < 50; i += 2 )
        T = Delete( i, T ); // 以 1 为步长，作删除操作

    // 测试删除操作是否成功
    for( i = 1; i < 50; i += 2 )
        if( ( P = Find( i, T ) ) == NULL || Retrieve( P ) != i )
            printf( "Error at %d
", i );
    for( i = 0; i < 50; i += 2 )
        if( ( P = Find( i, T ) ) != NULL )
            printf( "Error at %d
", i );

    // 打印最大数和最小数
    printf( "Min is %d, Max is %d
", Retrieve( FindMin( T ) ),
            Retrieve( FindMax( T ) ) );

    return 0;
}

测试结果：

定义错误的头文件 fatal.h

#include <stdio.h>
#include <stdlib.h>

#define Error(Str)        FatalError( Str )
#define FatalError(Str)   fprintf( stderr, "%s
", Str ), exit( 1 )

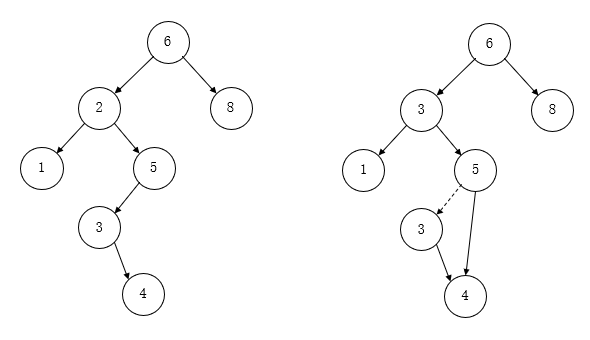
注：关于删除的操作的图解，用来备忘

删除具有 1 个儿子的节点 4 的前后情况：

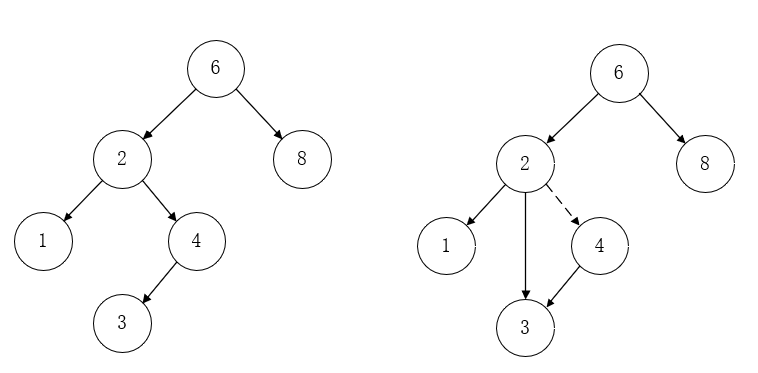
删除具有 2 个儿子的节点 2 的前后情况：