卡诺定理的证明

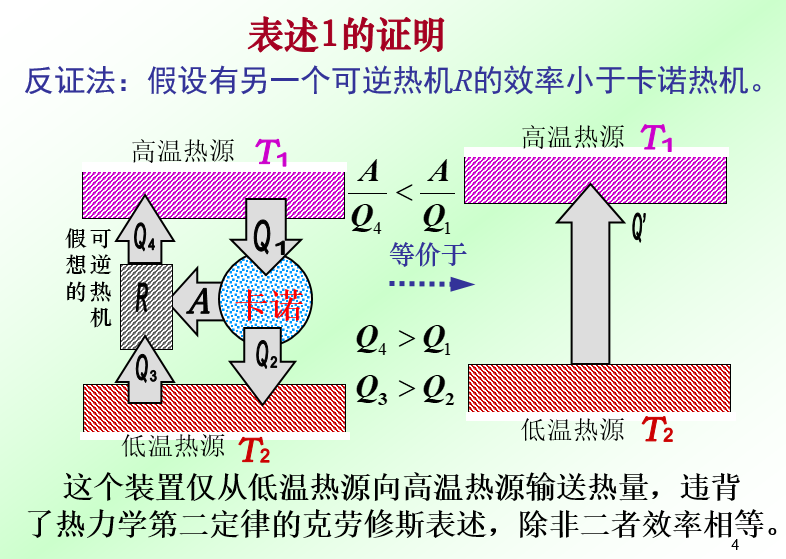
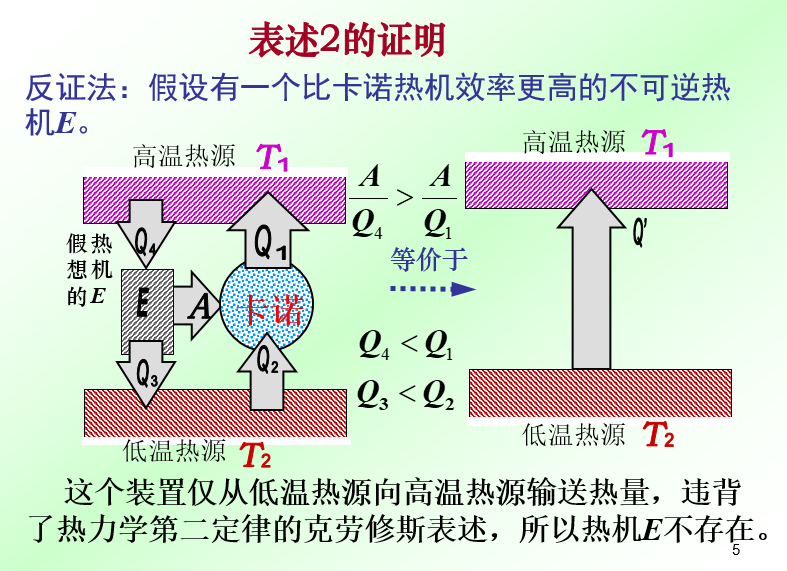
1、定义

2、证明

2.1、课堂上讲的证明

2.2、网络版证明

由于我对这个证明的理解有点模糊，所以又在网上重新找了一个证明，就是下面这个，结合一下就清晰了许多。

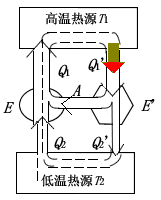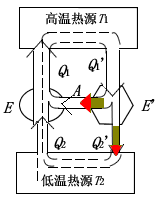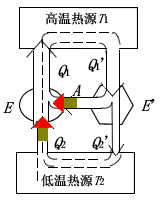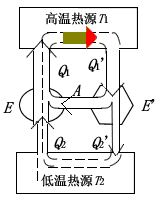
(1) 证明卡诺定理1：
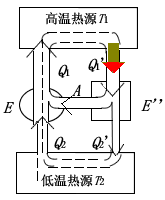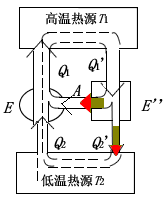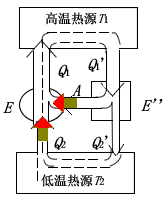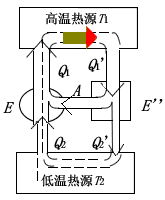
设有可逆机 (E) 和 (E')，令 (E') 作正循环，(E) 作逆循环，将它们组成复合机，如图所示，可以调节它们满足

[A = Q_1^{'} - Q_2^{'} = Q_1 - Q_2 qquad qquad ① ]

用反证法：先假设它们的效率 (eta^{'} > eta)，则

[displaystylefrac{Q_1^{'} - Q_2^{'}}{Q_1^{'}} > displaystylefrac{Q_1 - Q_2}{Q_1} qquad qquad ② ]

可得 (Q_2^{'} < Q_2, Q_1^{'} < Q_2)。

作为复合机，结果成为外界没有对复合机做功，而复合机却能将热量 (Q_2 - Q_2^{'} = Q_1 - Q_1^{'}) 从低温热源送到高温热源，这违背了热力学第二定律的克劳修斯表述。所以 (eta^{'} > eta) 为不可能，只有 (eta geq eta^{'})。类似地令 (E) 作正循环带动 (E^{'}) 作逆循环，可以证明 (eta > eta^{'}) 也是不可能的，只有 (eta^{'} geq eta)。可见两种结论相较，只有 (eta^{'} = eta) 成立。如果令 (E) 和 (E^{'}) 中任一热机为理想气体的可逆卡诺热机，即 (eta^{'} = eta = 1 - displaystylefrac{T_2}{T_1})。

(2) 证明卡诺定理2：
如下图所示，如果用一个不可逆机 (E^{''}) 来代替“证明卡诺定理1”中的可逆机 (E^{'})，并用 (E^{''}) 推动 (E) 工作，按同样方法，可以证明 (eta^{''} > eta) 是不可能的，即只有 (eta geq eta^{''})，由于 (E^{''}) 是不可逆机，因此无法证明 (eta leq eta^{''})，所以在相同的高低温两热源间工作的不可逆机的效率不可能大于可逆机的效率。