数据结构实验二 求整数幂和寻找数组主元问题的求解

一、求整数幂问题

1.问题描述

• 用基于2和3的方式分别写出算法来求 power(n, x)。分析两种算法的复杂程度，设计试验来验证你的想法。

2、问题分析与算法设计

问题：

• 如何使用较少的乘法次数求 (x^{27})？
• 方法：缓存中间结果，避免重复计算

过程演示：

[x^3 = x * x * x, x^9 = x^3 * x^3 * x^3, x^{27} = x^9 * x^9 * x^9 ]

[x^2 = x * x, x^4 = x^2 * x^ 2, x^8 = x^4 * x^4, x^{16} = x^8 * x^8, x^{27} = x^{16} * x^8 * x^2 * x ]

上面的方法利用的其实就是分治思想：

• 问题的规模是n，把n分解
• 如果n是偶数，(n = 2 * displaystylefrac{n}{2})；否则 (n = 2 * displaystylefrac{n}{2} + 1)
• 因此，(x^0 = 1)

3、实验方案/步骤

1. 声明求整数幂函数，其参数为 x, n，其中 x 代表底数，n 代表指数，在测试函数中通过改变传入的 x 和 n 的大小来获取不同的实验结果。
2. 定义 clock_t 类型的变量 start_time 并调用 clock() 函数来记录函数开始执行时间。
3. 定义求整数幂函数 power(n, x)，将 power() 函数放入一个循环次数为 1,000,000 的循环中，并执行。
4. 定义 clock_t 类型的变量 end_time 并调用 clock() 函数来记录函数执行结束时的时间。
5. 在控制台打印 (end_time - start_time)，此即函数执行 1,000,000次耗费的时间。
6. 重复 5 次实验，得到平均数据。
7. 记录相应的 10 组数据，并绘制对应的 Excel 图表。

4、算法实现

4.1、基于 2 的算法

递归代码实现

int power(int x, int n)
{
    if (0 == n)
        return 1;
    if (0 == n % 2) // 如果是偶数，就折半处理
        return power_2_Re(x * x, n / 2);

    return power_2_Re(x * x, n / 2) * x; // 奇数的情况要补乘一个 x
}

4.2、基于 3 的算法

递归代码实现

int power(int x, int n)
{
    if (n == 0)
        return 1;
    if (n == 1)
        return x;
    if (n == 2)
        return x * x;
    
    if (n % 3 == 0)
        return power(x * x * x, n / 3);
    if (n % 3 == 1)
        return power(x * x * x, n / 3) * x;
    
    return power(x * x * x, n / 3) * x * x;
}

4.3、全部代码

Power.h

#ifndef EXPALGORITHM_POW_H
#define EXPALGORITHM_POW_H

// 以二为底
int power_2_Re(int x, int n);
int power_2_Ite(int x, int n); // 迭代算法并没有进行测试

// 以三为底
int power_3_Re(int x, int n);
int power_3_Ite(int x, int n); // 同上

#endif //EXPALGORITHM_POW_H

Power.c

#include "Pow.h"

int power_2_Re(int x, int n)
{
    if (0 == n)
        return 1;
    if (0 == n % 2) // 如果是偶数，就折半处理
        return power_2_Re(x * x, n / 2);

    return power_2_Re(x * x, n / 2) * x; // 奇数的情况要补乘一个 x
}

int power_2_Ite(int x, int n)
{
    int res = 1;

    if (0 == n)
        return 1;

    for (; n > 0; n = n >> 1)
    {
        if (1 == n % 2)
            res *= x; // 奇数的情况下多出来的 x 对最后结果的贡献要保存在 res 中
        x *= x;
    }
    return res;
}

int power_3_Re(int x, int n)
{
    if (n == 0)
        return 1;
    if (n == 1)
        return x;
    if (n == 2)
        return x * x;

    if (n % 3 == 0)
        return power_3_Re(x * x * x, n / 3);
    if (n % 3 == 1)
        return power_3_Re(x * x * x, n / 3) * x;

    return power_3_Re(x * x * x, n / 3) * x * x;
}

int power_3_Ite(int x, int n)
{
    int res = 1;
    if (n == 0)
        return 1;

    for (; n > 0; n /=3, x = x*x*x)
    {
        if (n % 3 == 1) res *= x;
        if (n % 3 == 2) res *= x*x;
    }

    return res;
}

main.c

#include <stdio.h>
#include <time.h>
#include "Pow.h"


int main()
{

    clock_t start_time, end_time;

    start_time = clock();
    for (int i = 0; i < 1000000; ++i)
    {
        power_3_Re(2, 10000); // 这里放的是待执行采集数据的函数
    }
    end_time = clock();
    printf("time %ld ms
", (end_time - start_time));

    return 0;

}

5、测试结果记录

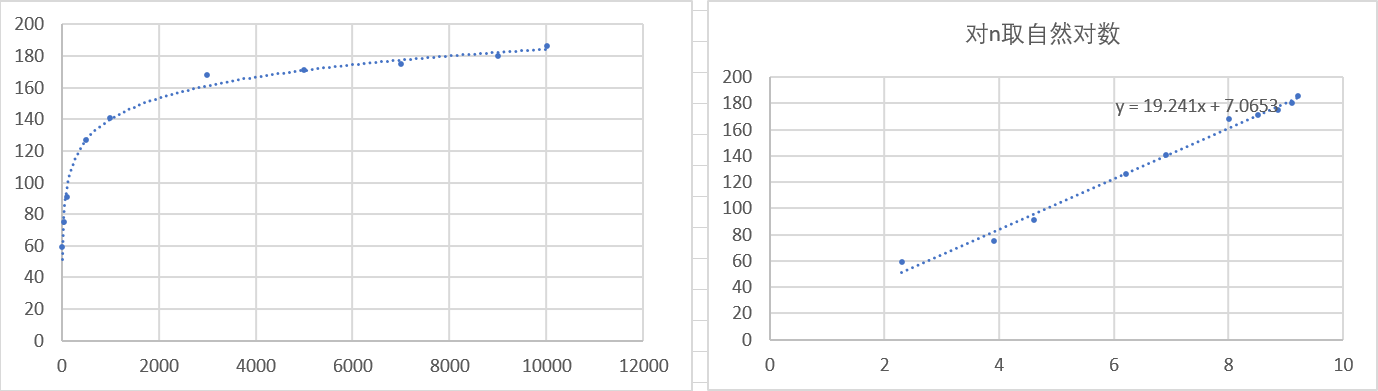
5.1、基于2求幂图表

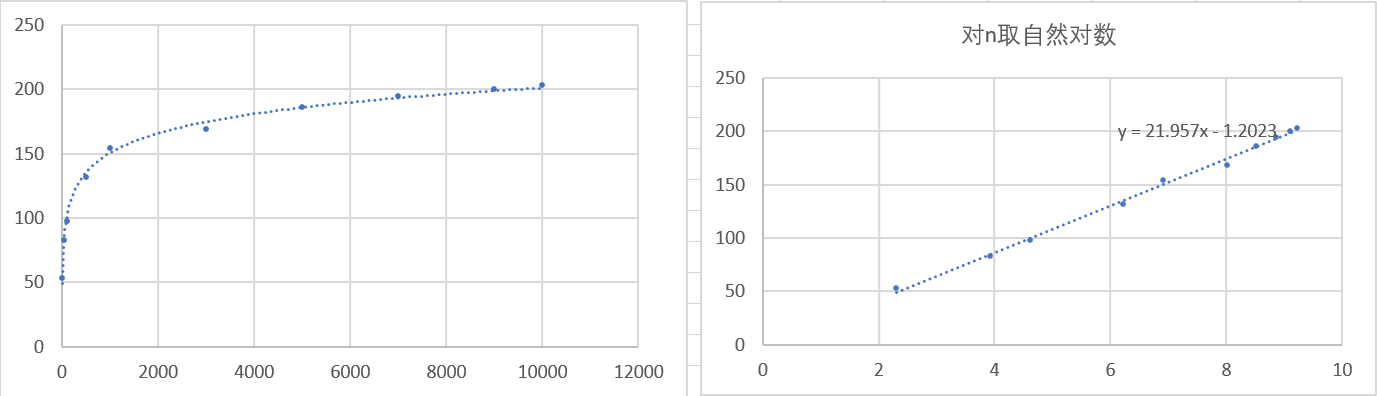
5.2、基于3求幂图表

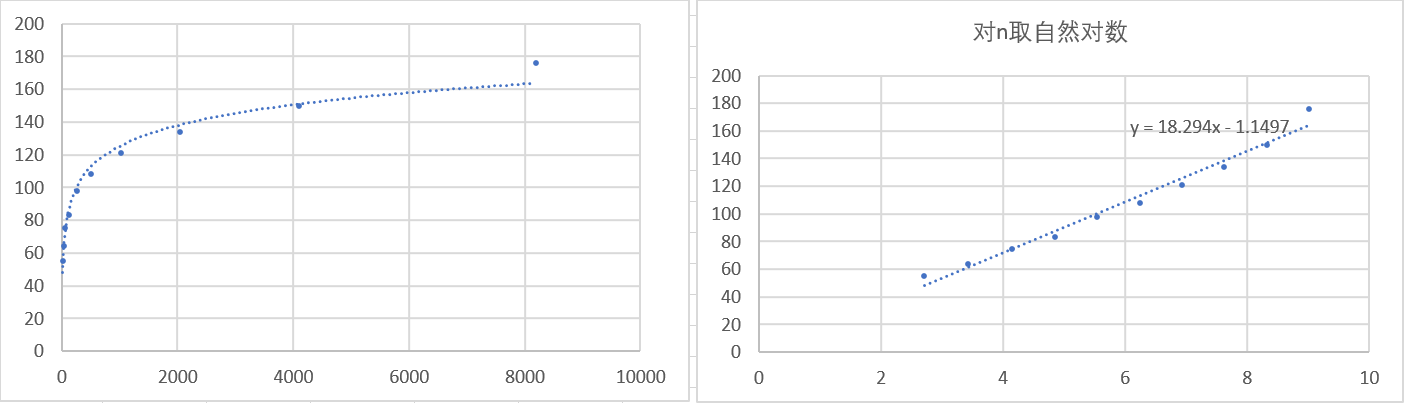
5.3、取最坏情况重新采集数据

基于2

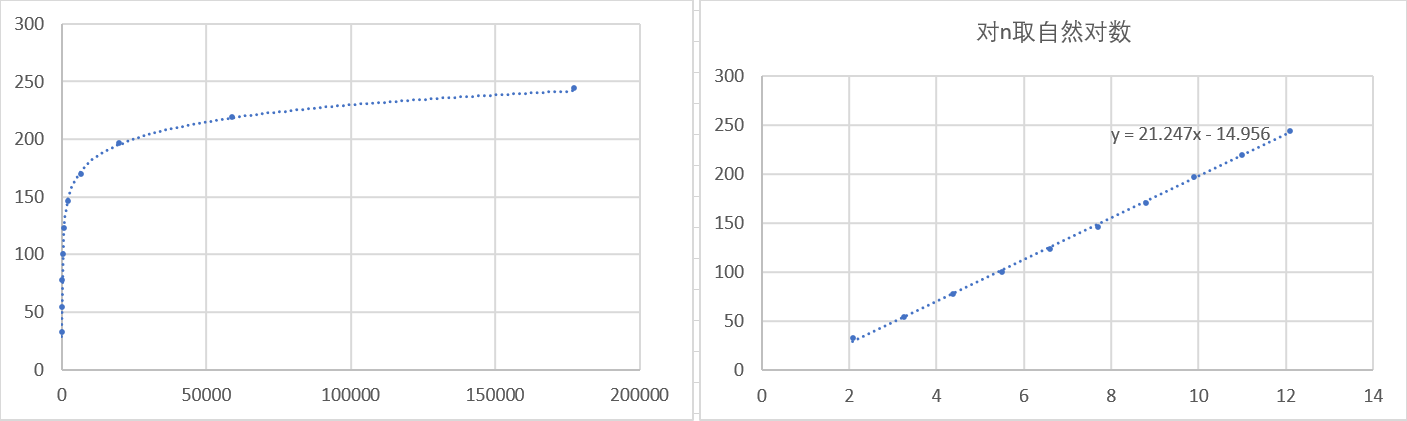
基于3

6、复杂度分析

根据理论分析，我们可以得出以2为底和以3为底的求幂函数时间复杂度即为递归的层数，即分别为 (O(log_2N)) 与 (O(log_3N)).

而我们根据实验数据拟合得到的的 n-t 曲线近似为对数曲线，(logn - t) 曲线近似为直线。以2为底、以3为底的时间复杂度分别为 (O(log_2N)) 与 (O(log_3N)) 与预期相符.

但是，我们可以发现一个问题，就是在理论分析的情况下，基于3的算法应该快于基于2的算法，可是，实验的结果却恰恰相反，其原因是C语言中作一次除以2的除法所花费的时间要小于除以3花费的时间很多。

二、求主元问题

1、问题描述(教材原文)

教材中的2.19

大小为N的数组A，其主要元素是一个出现次数超过N/2的元素（从而这样的元素最多有一个）。例如，数组3,3,4,2,4,4,2,4,4有一个主要元素4，而数组3,3,4,2,4,4,2,4没有主要元素。如果没有主要元素，那么你的程序应该指出来。

2、问题分析与算法设计

首先，找出主要元素的一个候选元（这是难点）。这个候选元是唯一有可能是主要元素的元素。第二步确定是否该候选元实际上就是主要元素，这正好是对数组的顺序搜索。为找出数组A的一个候选元，构造第二个数组B。比较A[1]和A[2]，如果它们相等，则取其中之一加到数组B中；否则什么也不做。以该方式继续下去直到读完这个数组。然后，递归地寻找B中的候选元；它也是A的候选元。

• 非分治算法：设置两重循环，将数组内的每一个元素与所有元素比较，若相同，则count++,若count>n/2,则该元素为主元，返回该元素。若循环结束还未满足条件，则返回0，表示没有找到主元。预计算法时间复杂度为 (O(n^2)) .

• 分治算法：采用递归，构造第二个数组B。比较A1和A2，若他们相等，则取其一加入B中，否则什么也不做。以该方式继续下去直到读完整个数组。然后对B数组重复上述操作。预计算法时间复杂度为 O(n)。

3、实验方案/步骤

1. 声明求主元函数，其参数为 x, n，其中 x 代表底数，n 代表指数，在测试函数中通过改变传入的 x 和 n 的大小来获取不同的实验结果。
2. 定义 clock_t 类型的变量 start_time 并调用 clock() 函数来记录函数开始执行时间。
3. 定义求整数幂函数 majEle_recursive(int a[], n)，将 majEle_recursive() 函数放入一个循环次数为 1,000,000 的循环中，并执行。
4. 定义 clock_t 类型的变量 end_time 并调用 clock() 函数来记录函数执行结束时的时间。
5. 在控制台打印 (end_time - start_time)，此即函数执行 1,000,000次耗费的时间。
6. 重复 5 次实验，得到平均数据。
7. 记录相应的 10 组数据，并绘制对应的 Excel 图表。

4、算法实现

#include <stdio.h>
#include <time.h>

#define NO_MAJ_ELE -1

int majEle_recursive(int a[], int n)
{
    int i, j, k = n / 2;
    int tmp;

    if (n == 0) return NO_MAJ_ELE;

    if (n == 1) return a[0];

    for (i = 0, j = 0; i < k; ++i)
    {
        if (a[2 * i] == a[2 * i + 1])
        {
            tmp = a[j];
            a[j++] = a[2 * i];
            a[2 * i] = tmp;
        }
    }

    tmp = majEle_recursive(a, j);
    if (n % 2 == 1) // 奇数的情况下，最后一个元素是候选元
    {
        if (tmp == NO_MAJ_ELE)
            return a[n - 1];
    }

    return tmp;
}

int main()
{
    // 测试数据，一共10组
    int a[10] = {1,2,1,2,1,2,1,2,1,1};
    int b[11] = {1,2,1,2,1,2,1,2,1,1,1};
    int c[12] = {1,2,1,2,1,2,1,2,1,1,3,3};
    int d[13] = {1,2,1,2,1,2,1,2,1,2,2,2,3};
    int e[14] = {1,2,1,2,1,2,1,2,1,1,3,3,3,3};
    int f[15] = {1,2,1,2,1,2,1,3,4,5,6,7,8,6,5};
    int g[16] = {1,2,1,2,1,2,1,3,4,5,6,7,8,6,5,2};
    int h[17] = {1,2,1,2,1,2,1,3,4,5,6,7,8,6,5,2,2};
    int i_1[18] = {1,2,1,2,1,2,1,3,4,5,6,7,8,6,5,2,3,3};
    int j[19] = {1,2,1,2,1,2,1,3,4,5,6,7,8,6,5,2,3,3,2};

    clock_t start_time, end_time;

    start_time = clock();
    for (int i = 0; i < 1000000; ++i)
    {
        // 手动改变测试数据
        majEle_recursive(j, 19);
    }
    end_time = clock();
    printf("time %ld ms
", (end_time - start_time));

    return 0;
}

5、测试结果记录

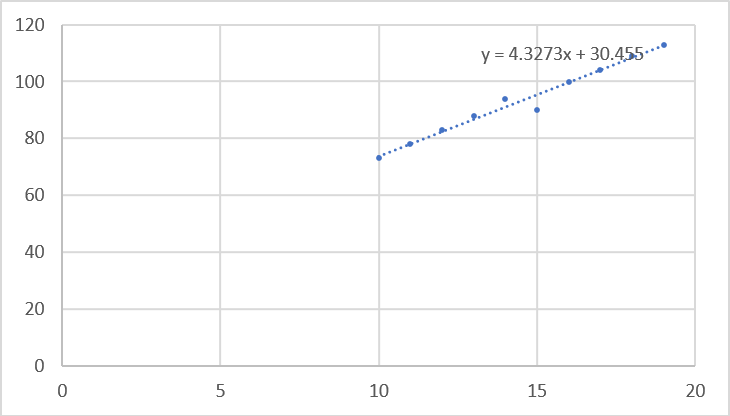
6、复杂度分析

前面经过理论分析，分治法求主元的的时间复杂度为 O(n)，观察实验数据，发现算法执行的时间与算法规模 n 成线性关系，与 O(n) 基本吻合。

如果我们使用非分治算法，即暴力求解，会使用两层循环，很显然，时间复杂度为 (O(n^2)).