求解圆上2N个点的连线问题(卡特兰数)

题目描述

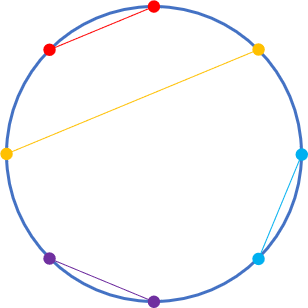
圆上有 2n 个不同的点, 两点之间连成直线段, 要求这些线段不能共点. 计算出有 12 个点时共有多少种不同的连线方式. 设计 C 语言函数, int count (int n), 计算并返回圆上有 2n 个点时的连线方式数量.

分析

我们可以使用动态规划的思想来求解这道题.

设 2n 个节点的连线方法种数为 (F(n)).

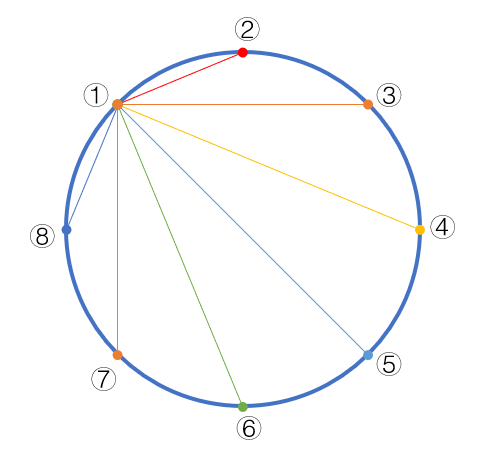
如上图(这里取 n = 4), 不妨给所有的点进行编号, 然后我们分析第一个节点, 发现从 1 号节点出发可以分为两种情况:

• 第一种: 1 和 2 或者 8 相连, 那么一共有 (2 imes F(2 imes 4 - 2)) 种连法.
• 第二种: 1 和 3 到 7 号的节点相连. 我们举个例子, 如果 1 号节点和 4 号相连, 那么, 这个圆就被分成了左下和右上两个部分(以黄色线为分割线), 此时有 (F(2) imes F(4)) 种连法. 把所有的情况累加, 一共有 (displaystylesum_{k = 2}^{4 - 1}F(2k - 2)F(8 - 2k)) 种连法.

上面的是一个特殊个例, 然后我们推到一般情况的公式就是:

[F(2n) = 2 imes F(2n - 2) + sum_{k = 2}^{n - 1}F(2k - 2)F(2n - 2k) ]

其中, (F(0) = 0, F(1) = 0, F(2) = 1).

代码

C语言实现

#include <stdio.h>
#include <string.h>

/**
 * 求解圆上 2N 个点连线问题
 * @param n 表示 2N, 为偶数
 * @return 结果数
 */
long count(int n)
{
    if (n == 2)
        return 1;

    long dp[n + 1];
    memset(dp, 0, (n + 1) * sizeof(long));

    dp[0] = dp[1] = 0;
    dp[2] = 1;
    for (int i = 4; i <= n; i += 2)
    {
        long sum = 0;
        for (int k = 4; k <= i - 2; k += 2) // 选 4, 6,..., n - 2 的情况
        {
            sum += (dp[k- 2] * dp[i - k]);
        }
        dp[i] = 2 * dp[i - 2] + sum; // 这里要加上选 1 和 选 n - 1 的情况
    }
    return dp[n];
}

int main() {

    // 打印 9 个测试数据
    for (int i = 2; i < 20; i += 2)
    {
        printf("%d
", count(i));
    }

    return 0;
}

测试结果:

1
2
5
14
42
132
429
1430
4862

Python实现

# -*- coding: utf-8 -*-
# @File  : CircleCatalan.py
# @Author: 模糊计算士
# @Date  : 2020/11/27

def count(n):
    if n == 2:
        return 1

    dp = [0] * (n + 1)

    dp[0] = dp[1] = 0
    dp[2] = 1
    for i in range(4, n + 1):
        sum = 0
        for k in range(4, i - 2 + 1):
            sum += dp[k - 2] * dp[i - k]
        dp[i] = 2 * dp[i - 2] + sum
        i += 2

    return dp[n]

for i in range(2, 100, 2):
    print(count(i))

测试结果:

1
2
5
14
42
132
429
1430
4862
16796
58786
208012
742900
2674440
9694845
35357670
129644790
477638700
1767263190
6564120420
24466267020
91482563640
343059613650
1289904147324
4861946401452
18367353072152
69533550916004
263747951750360
1002242216651368
3814986502092304
14544636039226909
55534064877048198
212336130412243110
812944042149730764
3116285494907301262
11959798385860453492
45950804324621742364
176733862787006701400
680425371729975800390
2622127042276492108820
10113918591637898134020
39044429911904443959240
150853479205085351660700
583300119592996693088040
2257117854077248073253720
8740328711533173390046320
33868773757191046886429490
131327898242169365477991900
509552245179617138054608572

从这些结果数据来看, 它们正是卡特兰数.