题目描述
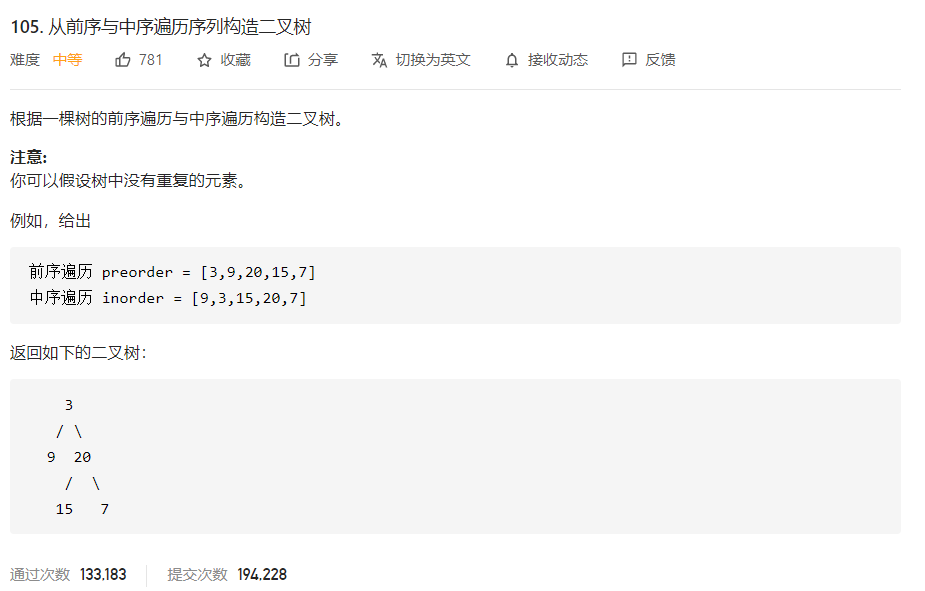
链接: https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
分析
二叉树前序遍历的顺序为:
- 先遍历根节点;
- 随后递归地遍历左子树;
- 最后递归地遍历右子树。
二叉树中序遍历的顺序为:
- 先递归地遍历左子树;
- 随后遍历根节点;
- 最后递归地遍历右子树。
在「递归」地遍历某个子树的过程中,我们也是将这颗子树看成一颗全新的树,按照上述的顺序进行遍历。挖掘「前序遍历」和「中序遍历」的性质,我们就可以得出根据前序和中序遍历构造二叉树的做法。
代码
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
struct TreeNode *newNode;
int p = 0;
int i = 0;
// 去除输入不合理的情况
if (preorder == NULL || inorder == NULL)
{
return NULL;
}
if (preorderSize <= 0 || inorderSize <= 0)
{
return NULL;
}
newNode = (struct TreeNode *) malloc(sizeof(struct TreeNode));
newNode->val = preorder[p]; // 根据前序取出根节点
newNode->left = NULL;
newNode->right = NULL;
for (i = 0; i < inorderSize; i++)
{
// 在中序中找到根节点,然后递归
if (inorder[i] == newNode->val)
{
newNode->left = buildTree(&preorder[p + 1], i, inorder, i); // 递归构造左子树
newNode->right = buildTree(&preorder[p + i + 1], preorderSize - i - 1, &inorder[i + 1],
inorderSize - i - 1); // 递归构造右子树
break;
}
}
return newNode;
}
完整的测试代码
#include <stdio.h>
#include <malloc.h>
// Definition for a binary tree node.
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
typedef struct TreeNode *BinTree;
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize)
{
struct TreeNode *newNode;
int p = 0;
int i = 0;
// 去除输入不合理的情况
if (preorder == NULL || inorder == NULL)
{
return NULL;
}
if (preorderSize <= 0 || inorderSize <= 0)
{
return NULL;
}
newNode = (struct TreeNode *) malloc(sizeof(struct TreeNode));
newNode->val = preorder[p]; // 根据前序取出根节点
newNode->left = NULL;
newNode->right = NULL;
for (i = 0; i < inorderSize; i++)
{
// 在中序中找到根节点,然后递归
if (inorder[i] == newNode->val)
{
newNode->left = buildTree(&preorder[p + 1], i, inorder, i); // 递归构造左子树
newNode->right = buildTree(&preorder[p + i + 1], preorderSize - i - 1, &inorder[i + 1],
inorderSize - i - 1); // 递归构造右子树
break;
}
}
return newNode;
}
void freeTree(struct TreeNode *T)
{
if (NULL == T)
return;
freeTree(T->left);
freeTree(T->right);
freeTree(T);
}
// 先序
void PreOrderTraversal(struct TreeNode *T)
{
if (T) {
printf("%d ", T->val);
PreOrderTraversal(T->left);
PreOrderTraversal(T->right);
}
}
// 中序
void InOrderTraversal(struct TreeNode *T) {
if (T) {
InOrderTraversal(T->left);
printf("%d ", T->val);
InOrderTraversal(T->right);
}
}
// 后序
void PostOrderTraversal(struct TreeNode *T) {
if (T) {
PostOrderTraversal(T->left);
PostOrderTraversal(T->right);
printf("%d ", T->val);
}
}
// 测试
int main()
{
int preorder[5] = {3, 9, 20, 15, 7};
int inorder[5] = {9, 3, 15, 20, 7};
BinTree buildedTree = buildTree(preorder, 5, inorder, 5);
printf("前序遍历:");
PreOrderTraversal(buildedTree);
printf("
");
printf("中序遍历:");
InOrderTraversal(buildedTree);
printf("
");
printf("后序遍历:");
PostOrderTraversal(buildedTree);
return 0;
}
输出结果:
前序遍历:3 9 20 15 7
中序遍历:9 3 15 20 7
后序遍历:9 15 7 20 3