Matlab 曲线拟合之polyfit与polyval函数

p=polyfit(x,y,n)

[p,s]= polyfit(x,y,n)

说明：x,y为数据点，n为多项式阶数，返回p为幂次从高到低的多项式系数向量p。x必须是单调的。矩阵s用于生成预测值的误差估计。

多项式曲线求值函数：polyval( )

调用格式： y=polyval(p,x)

[y,DELTA]=polyval(p,x,s)

说明：y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。

[y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y DELTA。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数。则Y DELTA将至少包含50%的预测值。

有如下数据

时间t	1900	1910	1920	1930	1940	1950	1960	1970	1980	1990	2000
人口y	76	92	106	123	132	151	179	203	227	250	281

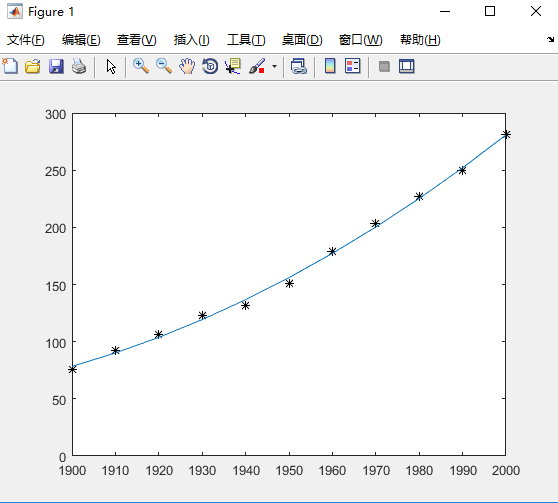
1. y与t的经验公式为 y = at^2 + bt + c

clear;
clf;                                                      %清除当前窗口
clc;
t = 1900:10:2000;                                         %时间t
y = [76 92 106 123 132 151 179 203 227 250 281];          %人口y

plot(t,y,'k*');
hold on;
% figure;       　　　　　　　　　　　　　　　　　　　　　　　　  %重新开一个图
p1 = polyfit(t,y,2);
plot(t, polyval(p1, t));
axis([1900 2000 0 300]);                                  %图像xy轴范围

disp(char(['y=',poly2str(p1,'t')],['a=',num2str(p1(1)),'   b=',...
    num2str(p1(2)),'   c=',num2str(p1(3))]));

结果如下：

y=   0.0094289 t^2 - 34.7482 t + 32061.5711
a=0.0094289   b=-34.7482   c=32061.5711

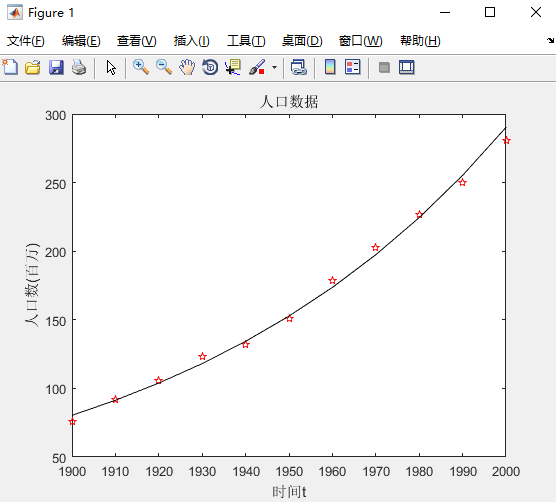
 2. y与t的经验公式为y = a e^(bt)

clear;
clf;                                                      %清除当前窗口
clc;
t = 1900:10:2000;                                         %时间t
y = [76 92 106 123 132 151 179 203 227 250 281];          %人口y
yy = log(y);                                              %指数基尼必需的线性化变形
p2 = polyfit(t,yy,1);
b = p2(1);
a = exp(p2(2));
y2 = a * exp(b*t);                                       %指数拟合函数式
plot(t,y,'rp',t,y2,'k-');
grid off;
xlabel('时间t');
ylabel('人口数(百万)');
title('人口数据');