Tetrahedron

Problem Description

Generate three integers a,b,and c in[1,n] with equal probability independently and use them as the three right-angle side length of a right-angled tetrahedron. Find the expectation of the reciprocal square of the distance from the right-angle apex to the slope(Euclidean distance).

For each test case ,output a line containing the answer mod 998244353

Input

In the first line, you should read an integer T denoting the number of test cases.

In every test case,the only line will include an integer n.

It is guaranteed that T is no larger than (2 imes 10^{6}) and n is no larger than (6 imes 10^{6}) .

Output

For each test case,output the only line containing just one integer denoting the answer mod 998244353

Sample Input

3
1
2
3

Sample Output

3
124780546
194103070

题解

#include<iostream>
#include<cstdio>
using namespace std;
#define mod 998244353 
long long F[6000005];
int T,n;
//快速幂 
long long pow(long long a,long long  b){
	long long ans=1;
	while(b){
		if(b&1){
			ans=ans*a%mod;
		}
		b>>=1;
		a=a*a%mod;
	}
	return ans;
}


int main(){
	//先打表求出逆元的前缀和 
	for(long long i=1;i<=6000005;i++){
		F[i]=(pow(i*i%mod,mod-2)+F[i-1])%mod;
	}
	scanf("%d",&T);	
	while(T--){
		scanf("%d",&n);	
		//输出 
		printf("%lld
",3*F[n]%mod*pow(n,mod-2)%mod);
	}
	return 0;
}

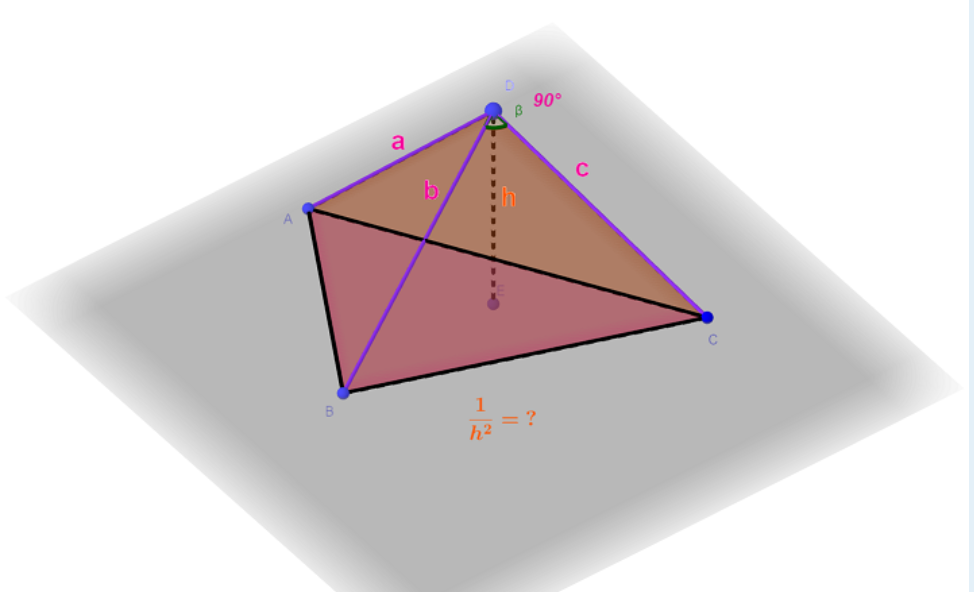
这题主要就是求期望，求(frac{1}{h^{2}}) 的期望，所以在此之前，我们要求出(frac{1}{h^{2}})用a、b、c表示的式子

• 设斜面三条边长度为(x,y,z)，面积为(S)，四面体体积为(V)

• 则(V=abc/6=Sh/3)，两边同时平方得到：

  [frac{1}{36} a^2 b^2 c^2=frac{h^2 S^2}{9} ]

• 海伦公式

  [S=sqrt{p(p-x)(p-y)(p-z)}, quad p=(x+y+z)/2 ]

• 代入得：

  [16 a^2 b^2 c^2=4 h^2 2p (2 p-2 x) (2 p-2 y) (2 p-2 z) \ 16 a^2 b^2 c^2=4 h^2 (x+y+z) (-x+y+z) (x-y+z) (x+y-z) ]

• 直接化简右边计算量较大，由于其是轮换对称的，考虑含(x)的项：(x^4,x^2y^2)的系数

  • 首先(x)的奇数次幂系数为(0)，因为(-(x+y+z) (-x+y+z) (-x+y-z) (x+y-z))，注意到前两项(x)加的内容是相同的，但是(x)本身符号不同，所以前两项中的(x)要么同时取，要么同时不取，否则就会被对方抵消，后两项也一样

  • (x^2 y z)系数为(0)，若取前两项的(x)，则是(-2yz)；取后两项的(x)，则是(2yz)，故是(0)

  • (x^4)系数为(-1)

  • (x^2y^2)系数为(2)，同样讨论两个(x)取自前两项还是后两项

  • 故

    [(x+y+z) (-x+y+z) (x-y+z) (x+y-z) = -sum_{cyc}x^4+2sum_{cyc}x^2y^2= sum_{cyc} x^2(2y^2-x^2) ]

• 勾股定理：

  [x^2=a^2+b^2 \ y^2=a^2+c^2 ]

• 代入得：

  [sum_{cyc} x^2(2y^2-x^2)=sum_{cyc}(a^2+b^2)(a^2-b^2+2c^2) \ sum_{cyc}(a^2+b^2)(a^2-b^2)+sum_{cyc}2(a^2+b^2)c^2 \ =2 sum_{cyc}(c^2a^2+b^2c^2)=4sum_{cyc}a^2b^2 ]

• [16 a^2 b^2 c^2=16 h^2 sum_{cyc}a^2b^2 \ ]

• 可得到(1/h^2=1/a^2+1/b^2+1/c^2)。
  我们可以直接记住这个公式，(frac{1}{h^{2}}=frac{1}{a^{2}}+frac{1}{b^{2}}+frac{1}{c^{2}}) ,下面附上一些直角四面体的性质。

得到这个公式后，我们可以得出：

(E(frac{1}{h^{2}})= E(frac{1}{a^{2}}+frac{1}{b^{2}}+{frac{1}{c^{2}}})=3 imes E(frac{1}{x^{2}}) ,xin [1,n]) ，x取整数

因为a、b、c都是相互独立的，所以(frac{1}{a^{2}}) 、(frac{1}{b^{2}}) 和(frac{1}{c^{2}}) 可以视为一个东西，我们这里用(frac{1}{x^{2}}) 来代替，x是从1~n中均匀随机选择的，然后前边乘以个3就行了。

那么现在我们就是要求(E(frac{1}{x^{2}})，xin [1,n]) ，x取整数就行了。

我们要求这个离散的变量的期望，那就用相应的结果乘以对应的概率，再求和。因为它是均匀随机分布的，所以概率固定是(frac{1}{n})所以可以得出以下式子：

(E(frac{1}{x^{2}})=(1 imes frac{1}{n}+frac{1}{4} imes frac{1}{n}+...+frac{1}{n^{2}} imes frac{1}{n}))

然后可以把(frac{1}{n}) 提出来

(E(frac{1}{x^{2}})=(1+frac{1}{4}+...+frac{1}{n^{2}}) imes frac{1}{n})

由于答案是要模一个数的，我们这里记作是模mod，所以可以写成

(E(frac{1}{x^{2}})=[(1+frac{1}{4}+...+frac{1}{n^{2}}) imes frac{1}{n}]\%mod)

(=[(1+frac{1}{4}+...+frac{1}{n^{2}})\%mod imes frac{1}{n}\%mod]\%mod)

(=[(1\%mod+frac{1}{4}\%mod+...+frac{1}{n^{2}}\%mod)\%mod imes frac{1}{n}\%mod]\%mod)

这个式子最后再乘一个3就是我们要求的东西了，我们可以发现这个式子中最基本的操作就是分数取模，那么也就需要求逆元，然后这个式子前边就是一个前缀和，照着这些写代码就行了。