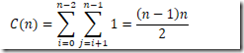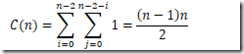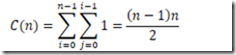蛮力法-选择排序、冒泡排序

时间总让我有后知后觉的挫感，或许是因为我从不愿记录过往。

3.1.1 选择排序（n个元素，0~n-1，升序，不稳定）

对数组A做i次扫描（0<=i<=n-2），每次从最后n-i个元素中寻找最小元素，然后将它与A_i交换。

代码实现

/**
     * 选择排序（升序）
     * @param array 排序的数组
     * */
    public static void selectSort(int[] array){
        for(int i=0;i<array.length-1;i++){
            int min=i;
            for(int j=i+1;j<array.length;j++){
                if(array[min]>array[j]){
                    min=j;
                }
            }
            if(min!=i){
                int temp=array[i];
                array[i]=array[min];
                array[min]=temp;
            }
        }
    }

算法分析

因此，对于任何输入来说，选择排序都是一个θ(n²)的算法。

 

3.1.1 冒泡排序（n个元素，0~n-1，升序，稳定）

比较相邻元素A_j和A_j+1，若A_j>A_j+1，交换它们的位置，依次这样，最终，最大元素“沉到”最后一个位置。重复n-1遍以后，就排好序了。

代码实现

/**
     * 冒泡排序（升序）
     * @param array 排序的数组
     * */
    public static void bubbleSort(int[] array){
        for(int i=0;i<array.length-1;i++){
            for(int j=0;j<array.length-1-i;j++){
                if(array[j]>array[j+1]){
                    int temp=array[j];
                    array[j]=array[j+1];
                    array[j+1]=temp;
                }
            }
        }
    }

算法分析

最坏情况和平均情况下都是属于θ(n²)。实际上，可以针对上面的代码进行一定的改良，当对数组迭代比较一遍之后没有进行元素的交换，那么表示该数组已排好序了。代码演示如下：

代码实现

/**
     * 冒泡排序（升序）
     * @param array 排序的数组
     * */
    public static void bubbleSort(int[] array){
        for(int i=0;i<array.length-1;i++){
            int count=0;
            for(int j=0;j<array.length-1-i;j++){
                if(array[j]>array[j+1]){
                    int temp=array[j];
                    array[j]=array[j+1];
                    array[j+1]=temp;
                    count++;
                }
            }
            System.out.println("第"+(i+1)+"次迭代：");
            print(array);//输出数组
            if(count==0){
                break;
            }
        }
    }

原本输出的结果：

排序前：
11,41,48,3,73,12,40,48,70,37
第1次迭代：
11,41,3,48,12,40,48,70,37,73
第2次迭代：
11,3,41,12,40,48,48,37,70,73
第3次迭代：
3,11,12,40,41,48,37,48,70,73
第4次迭代：
3,11,12,40,41,37,48,48,70,73
第5次迭代：
3,11,12,40,37,41,48,48,70,73
第6次迭代：
3,11,12,37,40,41,48,48,70,73
第7次迭代：
3,11,12,37,40,41,48,48,70,73
第8次迭代：
3,11,12,37,40,41,48,48,70,73
第9次迭代：
3,11,12,37,40,41,48,48,70,73
排序后：
3,11,12,37,40,41,48,48,70,73

改良后输出的结果：

排序前：
11,41,48,3,73,12,40,48,70,37
第1次迭代：
11,41,3,48,12,40,48,70,37,73
第2次迭代：
11,3,41,12,40,48,48,37,70,73
第3次迭代：
3,11,12,40,41,48,37,48,70,73
第4次迭代：
3,11,12,40,41,37,48,48,70,73
第5次迭代：
3,11,12,40,37,41,48,48,70,73
第6次迭代：
3,11,12,37,40,41,48,48,70,73
第7次迭代：
3,11,12,37,40,41,48,48,70,73
排序后：
3,11,12,37,40,41,48,48,70,73

可见，对上面的数组排序时，的确少了两次迭代。但事实上，即使在初等排序方法当中，冒泡排序也不是一个很好的选择，而且，如果不是因为它有一个好记的名字，我们很可能不会对它有任何的了解（这句话说得是不是很残忍，书的作者说的）。

习题 3.1

4. a.设计一个蛮力算法，对于给定的x0，计算下面多项式的值：

p(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀

_{并确定该算法的最差效率类型。}

    b.如果你设计的算法属于θ(n²)，请为该问题设计一个线性的算法。

    c.对于该问题来说，能不能设计出一个比线性效率还要好的算法呢？

解：

a.代码实现：

/**
     * 习题4.a 计算多项式p(x)
     * @param array 多项式的常数项
     * @param x 变量
     * @return 返回计算的结果
     * */
    public static int polynomialEvaluation(int[] array,int x){
        int result=0;
        for(int i=0;i<array.length;i++){
            int temp=array[i];
            for(int j=0;j<i;j++){
                temp*=x;
            }
            result+=temp;
        }
        return result;
    }

效率分析：

所以该算法属于θ(n²)。

b.代码实现：

/**
     * 习题4.b 计算多项式p(x)
     * @param array 多项式的常数项
     * @param x 变量
     * @return 返回计算的结果
     * */
    public static int polynomialEvaluation(int[] array,int x){
        int result=0;
        int temp=1;
        for(int i=0;i<array.length;i++){
            result+=array[i]*temp;
            temp*=x;
        }
        return result;
    }

c.由于该问题必须求解n+1个加数的和，所以不能设计出一个比线性效率还要好的算法。