Levenshtein distance,中文名为最小编辑距离,其目的是找出两个字符串之间需要改动多少个字符后变成一致。该算法使用了动态规划的算法策略,该问题具备最优子结构,最小编辑距离包含子最小编辑距离,有下列的公式。
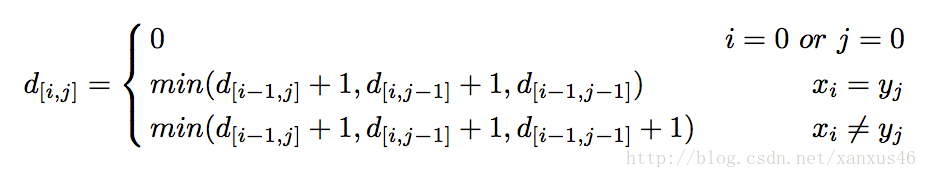
其中d[i-1,j]+1代表字符串s2插入一个字母才与s1相同,d[i,j-1]+1代表字符串s1删除一个字母才与s2相同,然后当xi=yj时,不需要代价,所以和上一步d[i-1,j-1]代价相同,否则+1,接着d[i,j]是以上三者中最小的一项。
算法实现(C#):
假设两个字符串分别为source,target,其长度分别为columnSize,rowSize,首先申请一个(columnSize+1)*(rowSize+1)大小的矩阵,然后将第一行和第一列初始化,matrix[i,0]=i,matrix[0,j]=j,接着就按照公式求出矩阵中其他元素,结束后,两个字符串之间的编辑距离就是matrix[rowSize, columnSize]的值,代码如下:
public class StringComparator { public static int LevenshteinDistance(string source, string target) { int columnSize = source.Length; int rowSize = target.Length; if (columnSize == 0) { return rowSize; } if (rowSize == 0) { return columnSize; }
int[,] matrix = new int[rowSize + 1, columnSize + 1]; for (int i = 0; i <= columnSize; i++) { matrix[0, i] = i; } for (int j = 1; j <= rowSize; j++) { matrix[j, 0] = j; }
for (int i = 0; i < rowSize; i++) { for (int j = 0; j < columnSize; j++) { int sign; if (source[j].Equals(target[i])) sign= 0; else sign = 1; matrix[i + 1, j + 1] = Math.Min(Math.Min(matrix[i, j] + sign, matrix[i + 1, j] + 1), matrix[i, j + 1] + 1); } } return matrix[rowSize, columnSize]; } public static float StringSimilarity(string source, string target) { int distance = LevenshteinDistance(source, target); float maxLength = Math.Max(source.Length, target.Length); return (maxLength - distance) / maxLength; } }