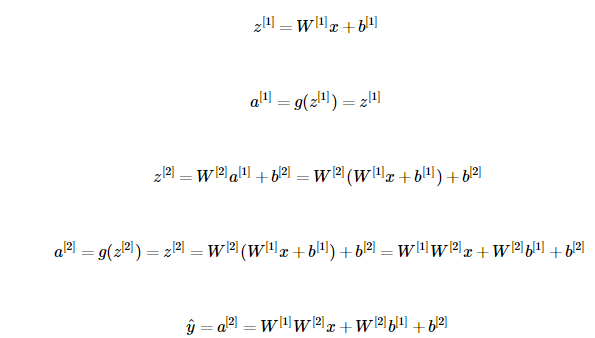激活函数

1. 什么是激活函数

  在神经网络中，我们经常可以看到对于某一个隐藏层的节点，该节点的激活值计算一般分为两步：
  （1）输入该节点的值为 x1,x2x1,x2 时，在进入这个隐藏节点后，会先进行一个线性变换，计算出值

　　　　　

 　　       上标 1表示第 1 层隐藏层。
   

2. 常用的激活函数

  在深度学习中，常用的激活函数主要有：sigmoid函数，tanh函数，ReLU函数。下面我们将一一介绍。

2.1 sigmoid函数

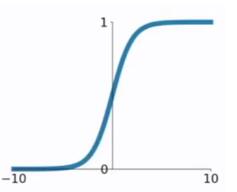
  在逻辑回归中我们介绍过sigmoid函数，该函数是将取值为 (−∞,+∞)(−∞,+∞) 的数映射到 (0,1)(0,1) 之间。sigmoid函数的公式以及图形如下：

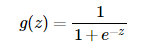
  对于sigmoid函数的求导推导为：

 

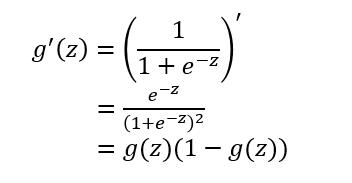
  sigmoid函数作为非线性激活函数，但是其并不被经常使用，它具有以下几个缺点：

   （1）当 z值非常大或者非常小时，通过上图我们可以看到，sigmoid函数的导数 g′(z) 将接近 0 。这会导致权重 W的梯度将接近 0，使得梯度更新十分缓慢，即梯度消失。

　　　　　　下面我们举例来说明一下，假设我们使用如下一个只有一层隐藏层的简单网络：

 

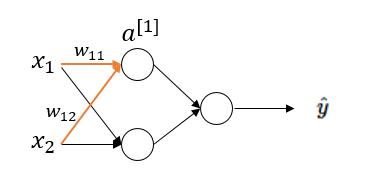
   　　　　　　对于隐藏层第一个节点进行计算，假设该点实际值为 a ，激活值为 a[1]。于是在这个节点处的代价函数为（以一个样本为例）：

   　　　　　　而激活值 a[1]的计算过程为：

   　　　　　　于是对权重 w11 求梯度为：　　　

 　　　　
   （2）函数的输出不是以0为均值，将不便于下层的计算，具体可参考引用1中的课程。sigmoid函数可用在网络最后一层，作为输出层进行二分类，尽量不要使用在隐藏层。

2.2 tanh函数

  tanh函数相较于sigmoid函数要常见一些，该函数是将取值为 (−∞,+∞) 的数映射到 (−1,1) 之间，其公式与图形为：　　

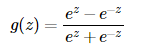
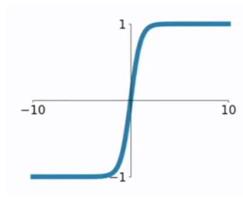
  tanh函数在 0 附近很短一段区域内可看做线性的。由于tanh函数均值为 0 ，因此弥补了sigmoid函数均值为 0.5 的缺点。
  对于tanh函数的求导推导为：

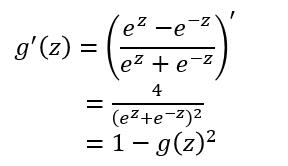
  tanh函数的缺点同sigmoid函数的第一个缺点一样，当 z 很大或很小时，g′(z)接近于 0，会导致梯度很小，权重更新非常缓慢，即梯度消失问题。

2.3 ReLU函数

  ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题。ReLU函数的公式以及图形如下：

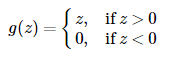
  对于ReLU函数的求导为：　　　　　　　　

  ReLU函数的优点：

   （1）在输入为正数的时候（对于大多数输入 zz 空间来说），不存在梯度消失问题。
   （2） 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）
  ReLU函数的缺点：
   （1）当输入为负时，梯度为0，会产生梯度消失问题。

2.4 Leaky ReLU函数

  这是一种对ReLU函数改进的函数，又称为PReLU函数，但其并不常用。其公式与图形如下：　　

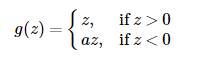
  其中 a 取值在 (0,1)之间。Leaky ReLU函数的导数为：
  　　　　　　　　　　

  Leaky ReLU函数解决了ReLU函数在输入为负的情况下产生的梯度消失问题。

3. 为什么要用非线性激活函数？

  我们以这样一个例子进行理解。
  假设下图中的隐藏层使用的为线性激活函数（恒等激活函数），也就是说 g(z)=z 。

  于是我们可以得出：

  可以看出，当激活函数为线性激活函数时，输出 y^ 不过是输入特征 x 的线性组合（无论多少层），而不使用神经网络也可以构建这样的线性组合。而当激活函数为非线性激活函数时，通过神经网络的不断加深，可以构建出各种有趣的函数。