Z变换(Z-transform) 将离散系统的时域数学模型——差分方程转化为较简单的频域数学模型——代数方程,以简化求解过程的一种数学工具。Z是个复变量,它具有实部和虚部,常常以极坐标形式表示,以Z的实部为横坐标,虚部为纵坐标构成的平面称为Z平面,即离散系统的复域平面。离散信号系统的系统函数(或者、称传递函数)一般均以该系统对单位抽样信号的响应的Z变换表示。由此可见,Z变换在离散系统中的地位与作用,类似于连续系统中的拉氏变换。
从数学的角度来看,Z变换只是信号的一种替代表示。
对于离散信号x(n),其Z变换定义如下:
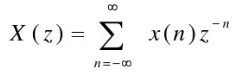
将复变量z表示成极坐标形式:
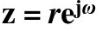

Z平面为横坐标为Z变量的虚部纵坐标为Z变量实部:

Z变换公式中,令![]() ,可以得到离散序列的傅里叶变换与Z变换的关系:
,可以得到离散序列的傅里叶变换与Z变换的关系:
线性:

时移:

Z变换的收敛域ROC(Region of Covergence):
对于给定的序列x[n]满足条件

Z反变换:
部分分式展开,
对于有理函数形式的X(z),可表示成:


若M<N,并且所有的极点是一阶的,可进行部分和展开成为:
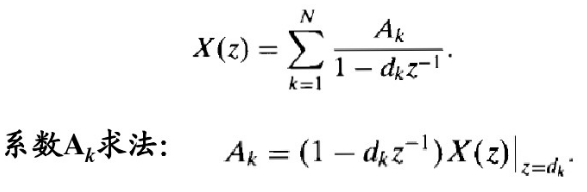
对于
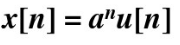

零点为0,极点为a.
收敛条件为:

收敛域为:

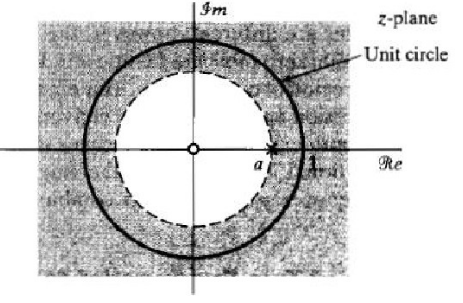
|a|<1, x[n]收敛,|a|=1,等幅震荡, |a|>1, 发散
在 z 平面上,系统函数的极点可能位于单位圆内、单位圆上或者单位圆外。对于一个因果系统而言,如果极点位于单位圆内,冲激响应的将随 n 值的增大而衰减;如果极点在单位圆上,冲激响应的将不随 n 值的大小而改变,它是一个等幅的变化;如果极点在单位圆外,冲激响应的将随 n 值的增大而增大。
系统函数:
设系统的N阶线性常系数差分方程为
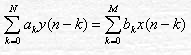
双边Z变换:

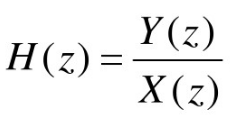
H(Z)被称为系统函数。
对H(Z)进行Z逆变换即得到单位采样响应。
对于该系统其他输入信号的响应,可以将输入信号进行Z变换然后乘以H(Z),再进行Z逆变换。