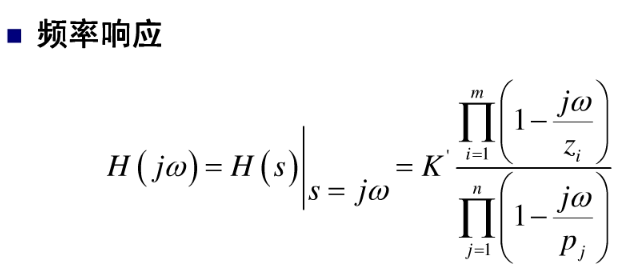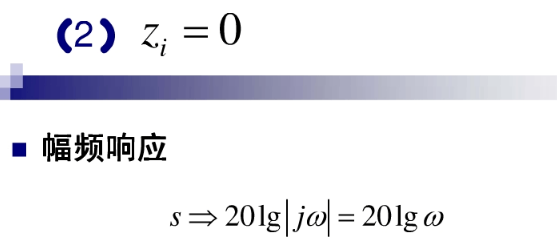转自:
https://www.zhihu.com/question/22085329
https://wenku.baidu.com/view/691d4629640e52ea551810a6f524ccbff121cac4.html
https://wenku.baidu.com/view/fc07dd563b3567ec102d8a52.html
https://wenku.baidu.com/view/501b7d11336c1eb91a375dbe.html?from=search
定义:
连续时间傅里叶变换的公式是:
这里的是实数。
傅里叶变换要求时域信号绝对可积,即
为了让不符合这个条件的信号,也能变换到频率域,我们给x(t)乘上一个指数函数,
为任意实数。
可以发现,这个函数,就满足了绝对可积的条件,即
关于为什么满足绝对可积条件,这里提一下,感性地说,我们知道负指数函数随t的增大,趋于零的速度是所有函数中最快的,这也是为什么我们描述某个现象暴涨的时候会说指数上升。因此大多数一般的函数
乘上某个负指数函数之后,一定绝对可积。
用更加严谨的数学表达,对于大多数,
,使得
是
的高阶无穷小。即
。因此在
的压迫下,
就满足了绝对可积的条件。
于是这个新函数的傅立叶变换就是:
化简得
显然是一个复数,我们把这个复数定义为一个新的变量——复频率,记为s。
于是便得到了拉普拉斯变换的公式:
所以拉普拉斯变换与连续时间傅里叶变换的关系是:拉普拉斯变换将频率从实数推广为复数,因而傅里叶变换变成了拉普拉斯变换的一个特例。当s为纯虚数时,x(t)的拉普拉斯变换,即为x(t)的傅里叶变换。
传递函数:
对于最简单的连续时间输入信号 x(t), 和输出信号 y(t)来说传递函数 H(s)所反映的就是零状态条件下输入信号的拉普拉斯变换X(s) 与输出信号的拉普拉斯变换 Y(s) 之间的线性映射关系:

系统收敛条件:
传递函数可以分解为以下形式:

Sp为r重极点,Si为一阶极点。
反变换得到系统冲激响应:

当极点在jw左半平面时,系统是稳定的(收敛)。










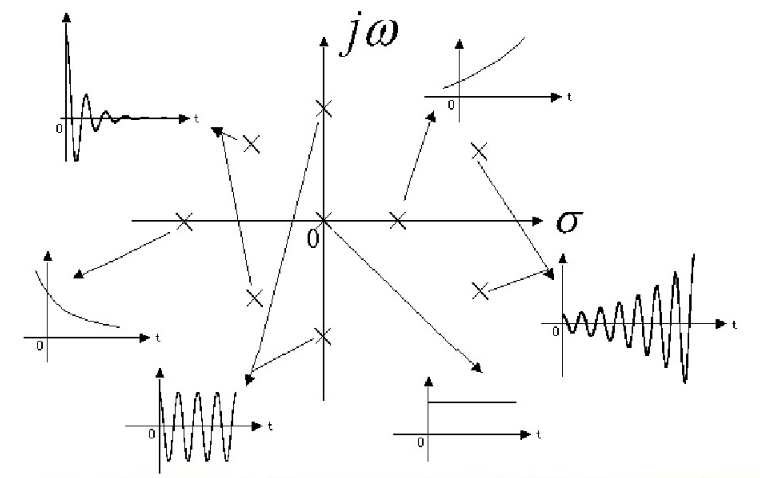
系统频率响应:
s=jw,即为系统的傅里叶变换,即为系统的频率响应。频率响应函数可以表示成零极点的形式。
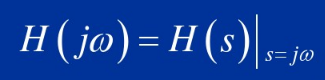


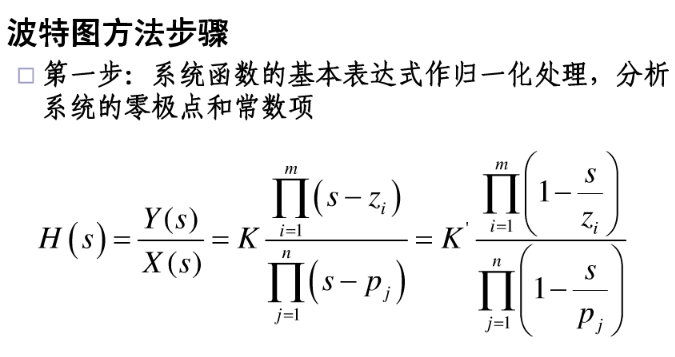
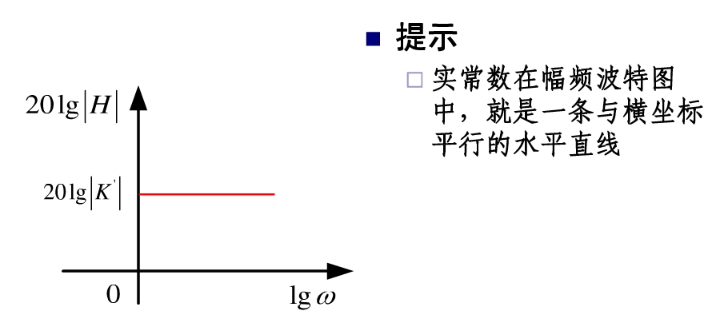
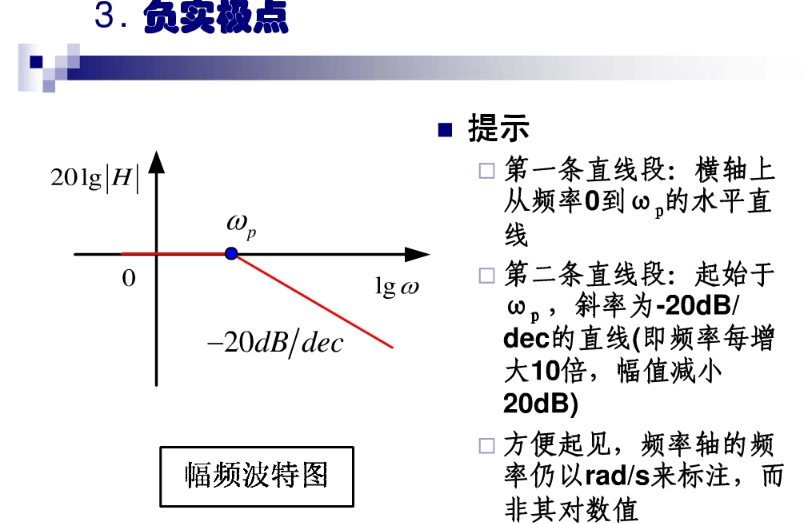
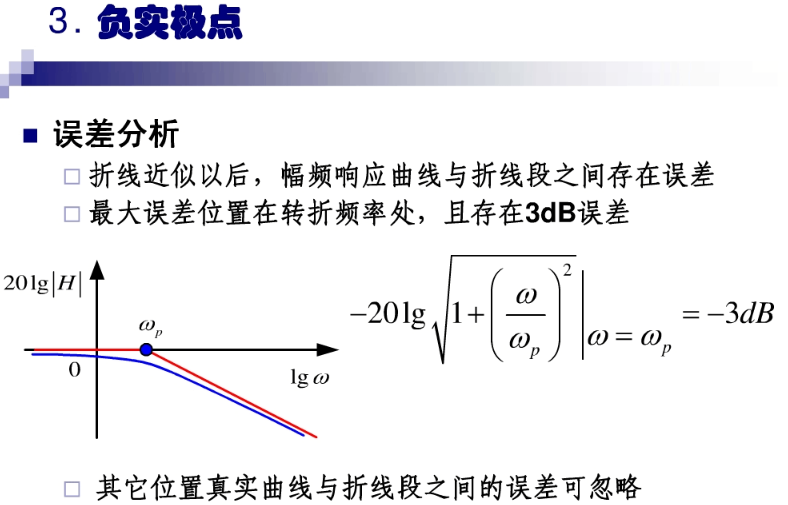
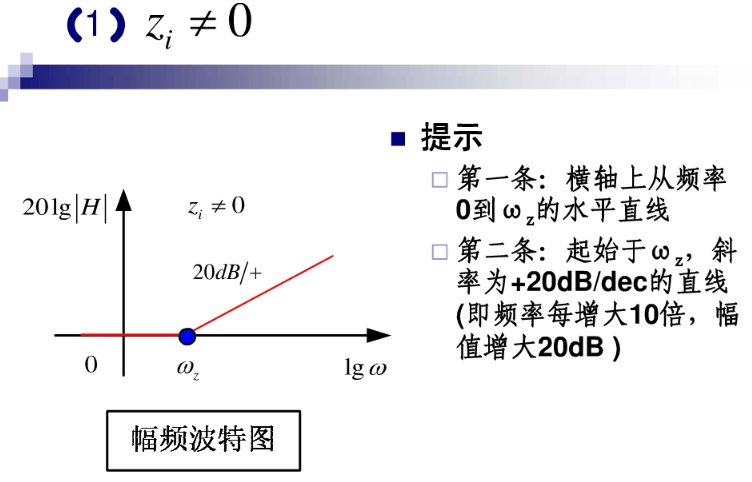
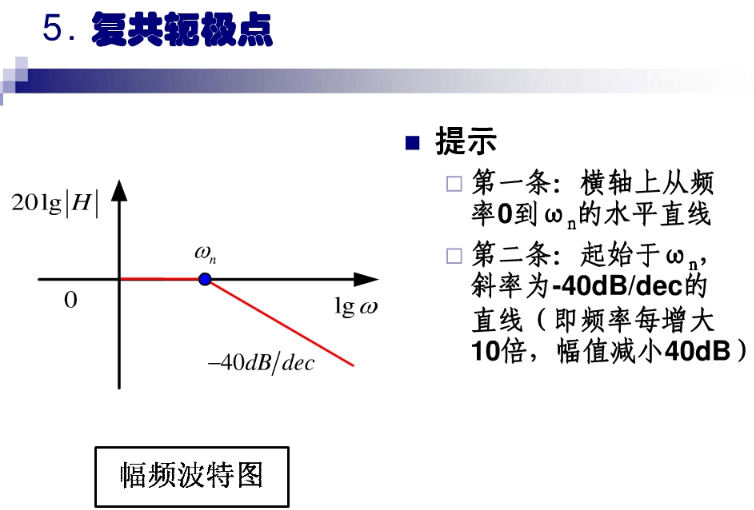
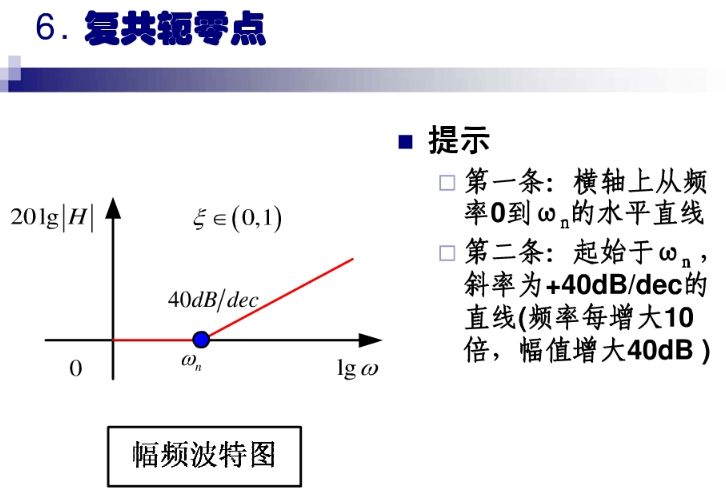
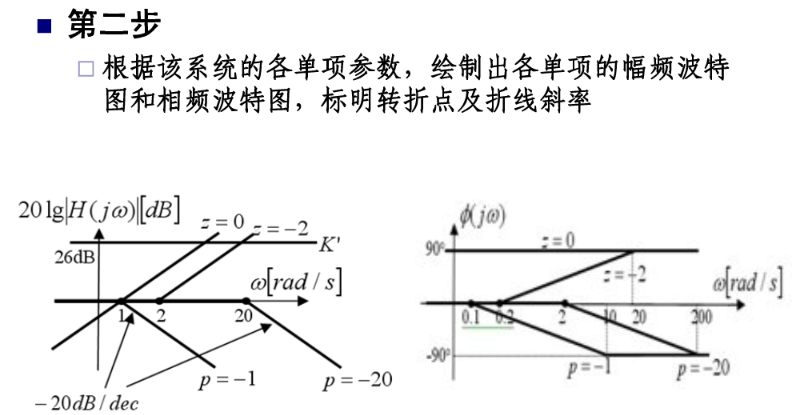
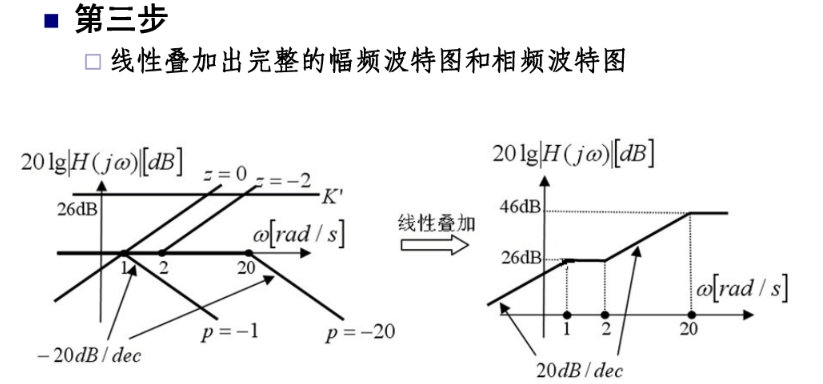
波特图: