KMP字符串匹配算法

1. KMP算法用途

KMP算法用于解决主字符串和模式字符串匹配的问题。如果完成匹配，返回模式字符串在主字符串匹配的初始索引。如果不匹配，返回-1。

2. PMT(Partial Match Table)：部分匹配表（模式字符串）

部分匹配表是KMP算法的核心，定义：前缀集合和后缀集合交集中最长元素的长度。

前缀集合：如果字符串M = A + S，A和S非空，则A是M的一个前缀，所有的前缀组成前缀集合。

后缀集合：如果字符串M = A + S，A和S非空，则S是M的一个后缀，所有的后缀组成后缀集合。

图中表示了Index = 10时，PMT = 4的计算过程，前缀字符串abab与后缀字符串abab匹配。

3. KMP算法实现

如果主字符串是T，匹配字符串是P，T[ i ] != P[ j ]时，此时可以通过右移匹配字符串PMT[ j - 1 ]个单位来解决，即令 j = PMT[ j - 1]

如果T[ i ] = P[ j ]，则i++, j++，表示目前匹配

如果T[ i ] != P[ j ]

　　如果 j == -1，则需要 i++, j++，j++ 表示P 从0开始匹配，i++表示当前不匹配，从下一个位置开始匹配。

　　如果 j != -1，则从后缀字符串与前缀字符串已经匹配，令 j = next[j]即可。

循环结束，当 j == strlen(p)时，表示完全匹配，此时返回 i - j 表示匹配的起始位置。

例：主字符串："abababcab"，子字符串："ababc"

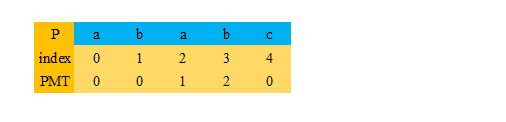
匹配过程：

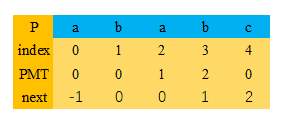
为了简化计算，引入next数组记录 j 索引处 PMT[ j - 1 ]的数值。

代码实现

int KMP(char * t, char * p) 
{
    int i = 0; 
    int j = 0;

    while (i < strlen(t) && j < strlen(p))
    {
        if (j == -1 || t[i] == p[j]) 
        {
            i++;
                   j++;
        }
         else 
                   j = next[j];
        }

    if (j == strlen(p))
       return i - j;
    else 
       return -1;
}

4. PMT, next实现过程

通过移动与自身字符串匹配求next：

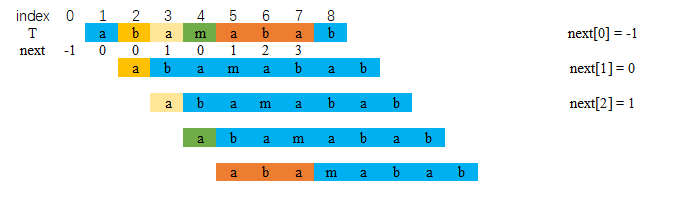
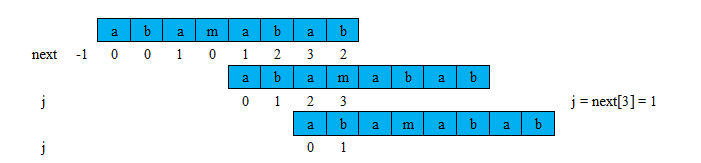
注意:如果不匹配，j 的值应该设为：next[j]，继续向下匹配，直到为 j = -1 为止再从0开始匹配，下图说明了原因。

 

代码实现：

void getNext(char * p, int * next)
{
    next[0] = -1;
    int i = 0, j = -1;

    while (i < strlen(p))
    {
        if (j == -1 || p[i] == p[j])
        {
            ++i;
            ++j;
            next[i] = j;
        }    
        else
            j = next[j];
    }
}