旋转已排序数组中查找

1. 数组中无重复元素

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Your algorithm's runtime complexity must be in the order of O(log n).

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

1.1 寻找最小值所在的点
建立模型求解

本题关键在于求解 最小值所在的索引，再通过二分法求解即可。

选择right作为比较的轴值，原因在于nums[right] 永远不会等于nums[mid]，分一下三种情况讨论。

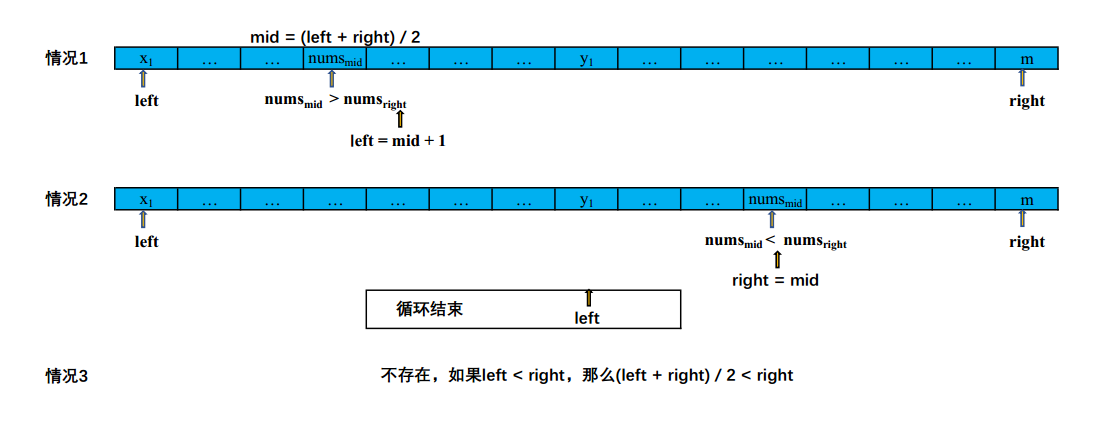
如果中间值比最右端的值大，那么应该让 left = mid + 1，如果中间值比最右端小，那么应该让right = mid，因为nums[mid] = y1时也是满足中间值比最右端小，不应该让right = mid - 1.

循环结束时left = right = index(y1)

 1.2 二分法求解

先按照标准的二分法思路求解，不同的是，旋转以后，中间值与未旋转之前总是向后偏移最小值索引个单位。

 int search(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1;
    int mid = 0;

    while (left < right) {
        mid = (left + right) / 2;
        if (nums[mid] <= nums[right]) {
            right = mid;
        }
        else {
            left = mid + 1;
        }
    }
    int point = left;
    left = 0;
    right = nums.size() - 1;
    while (left <= right) {
        int medium = (left + right) / 2;
        mid = (medium + point) % nums.size();
        if (nums[mid] < target) {
            left = medium + 1;
        }
        else if (nums[mid] > target) {
            right = medium - 1;
        }
        else {
            return mid;
        }
    }
    return -1;
}