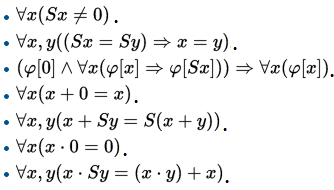上帝所做的、胜过一切想象中的幸福行为,莫过于纯粹的思考,而人的行为中最接近这种幸福的东西,也许是与思考最密切的活动。
——亚里士多德
逻辑作为一种思维和认知方式,对现代人的学习和生活都是必不可少的。人们日常的交流讨论需要逻辑;新知识、新技能的学习需要逻辑;保障人们有序生活、工作的各种规章制度、法律条文的表述也都基于逻辑。逻辑在人们学习、工作和生活中的重要作用已得到广泛认可,许多家长都注重从小培养孩子的逻辑思维能力。那么,究竟什么是逻辑呢?
逻辑(英文logic)一词来源于古希腊语(λογική),其最初的意思是“话语”,之后逐渐被用于描述思考或推理的过程和方式,即通过一些确定的思维“模式”建立起连接假设与结论的纽带。这种朴素的思考和推理方式长期被古希腊学者用于演讲和辩论。而后逐渐被人们用于哲学、数学以及各种自然科学的研究。
|
|
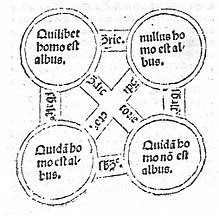
图1 逻辑方阵(15世纪)
逻辑含义的演化反映了人们对思维认识的深化。古希腊思想家认为,只有通过这种“逻辑”思考才能领悟物质世界的实质和精髓。柏拉图认为,人可以通过对物质世界的观察抽取基本真理,再通过理性的(逻辑)思考探究世界的规律。正是通过这种“思考”,人们能够从正确的前提出发,获得正确可靠的结论。更进一步,亚里士多德认为,逻辑是自然科学研究的基础,因而需要将“理性的思考”与具体物质世界的真理相分离。为此,他提出了著名的三段论、反证法等逻辑推演法则。
亚里士多德所开创的逻辑也被称为亚里士多德逻辑,在随后近两千年的历史进程中广为传播,长期被人们视为哲学思考和研究的基本思维方式,促进了自然科学的发展。特别是对于数学的发展,它起到了至关重要的作用:指明了从公理和定义出发,由逻辑推理建立一套严格理论体系的途径和方法。正是基于这种逻辑推理的方法,欧几里得的《几何原本》才成了构建数学知识大厦的不朽典范。
|
|
图2 1573年版《几何原本》
十七世纪后期,德国数学家戈特弗里德·威廉·莱布尼茨首先提出,要建立一种“通用的形式语言”,用于描述数学推理。在这种语言中,每个概念都应该用一个符号表示;这样,抽象的“思维过程”就可以通过机械的“符号演算”来处理。尽管莱布尼茨没有明确给出现代逻辑的表示方式,但他提出的这种形式语言和符号演算的思想却正是现代数理逻辑的主要特征。
到了十九世纪中叶,逻辑终于从“论证”的手段转变为处理数学问题的系统方法。1854年,乔治·布尔出版了《The Laws of Thought》,首次从代数系统的角度阐述了逻辑推演方法。布尔接受了亚里士多德逻辑的主要观念,并对传统逻辑进行了系统化推进:扩展了命题的数量,提供了抽象的逻辑推演规则,加入了数学最基本的符号——等词。该代数系统就是著名的布尔代数,它是现代命题逻辑和计算机科学的基础。
1879年,戈特洛布·弗雷格发表了《概念文字》(Begriffsschrift)。他在命题逻辑中引入量词(“全部(任意)”、“一些(存在)”)符号,将原本简单的命题符号扩充为带有量词的谓词语句。这种扩展大大增强了逻辑的表达能力,使得许多数学分支都可以由该(一阶)逻辑系统的形式语言去刻画。例如,基于若干公理构建的自然数算数系统(皮亚诺算术)就可以通过一阶逻辑完全刻画(见图4)。至此,“数理逻辑”的概念和理论逐步形成。
|
|
图3 皮亚诺算数公理的一阶逻辑表示
数理逻辑是用数学方法研究逻辑的学问,它既包含数学推理的抽象规则,又为具体数学知识的描述提供形式语言,是现代数学必不可少的组成部分。
随着数学知识的不断扩充,要将所有数学结论列举出来似乎并不可行。人们转而期望能够选择有限多个不证自明的数学论断作为初始公理,通过逻辑推理获得所有其他数学结论。1900年,戴维·希尔伯特在巴黎国际数学家大会上作了题为《数学问题》的报告,提出了23个著名的数学问题。其中第二个问题就是希望能以严谨逻辑推理的方式证明任意公理系统内命题的相容性(一致性)。
1910年到1913年,伯特兰·罗素和他的老师阿尔弗雷德·怀特海德合著了《数学原理》,期望根据有限的数学公理,通过与具体领域无关的逻辑推理获得各个数学领域中的全部真理。这就要求数学公理系统具有两个重要性质:可靠性(即所有可证的数学命题都是正确的)和完备性(即所有为真的数学命题都是可证的)。
1929年,库尔特·哥德尔证明了一阶逻辑系统自身的完备性,其可靠性也可以证明。看上去,一切似乎都十分顺利。然而,在1931年他又证明了著名的哥德尔不完备定理,指出皮亚诺算数系统具有不完备性,从根本上否定了通过严格逻辑证明获得全部数学定理的可能性;稍微复杂些的数学公理系统(如包含皮亚诺算术的公理系统)都会存在不能被证明的命题。这一结论击碎了几代数学家的梦想,同时也说明了形式化语言的局限性。
1936年和1937年,阿隆佐·邱奇和艾伦·麦席森·图灵基于各自的计算模型——lambda演算和图灵机,再次从可计算的角度分别独立地给出了希尔伯特第二问题的否定答案,即,不存在一个通用的算法,它可以用于判定任何一个数学命题是否为真。
|
|
图4 不完备定理的经典对角线构造
尽管哥德尔、邱奇和图灵对数学公理系统的完备性给出了否定答案。然而,他们的工作却为数学研究打开了另外一扇大门——可以根据具体需要选择恰当的断言作为初始公理,使得数学向着更为广阔的领域发展。目前,数理逻辑正在沿着四个相互独立却又内部关联的方向——模型理论、证明理论、可计算性和集合论——不断发展,继续夯实现代数学和计算机科学的理论基础。
随着计算机和移动设备计算能力的不断提升,数理逻辑在定理自动证明、程序验证、知识管理、数学计算中的作用日益突显,为数学机械化、算法数学、计算机应用、人工智能等学科之间的立体交叉提供了基石、架起了桥梁;同时,数学与计算机科学的交叉融合也在促使数理逻辑自身不断地向前发展。
(文中图片来自百度百科、维基百科等网上资料;感谢阿狗数学AlgoMath的老师和同学们对文章内容、措辞的修改和建议)
(北京林业大学信息学院 蒋东辰)
来源:阿狗数学AlgoMath