Typeclassopedia 阅读笔记
本文是对介绍 Haskell 中类型类(type classes)的文档 Typeclassopedia 的阅读笔记和简短总结,包含此文档中重要的知识点。读者请配合原文档阅读使用。
注意事项
首先,Typeclassopedia 并非介绍 Haskell 基础的新手教程,假设读者已熟练掌握 Haskell 基础知识(Haskell 初学者推荐首先阅读 Learn You a Haskell for Great Good)。
笔者接触 Haskell 时间尚短,所作总结难免有所遗漏或偏颇,欢迎及时提出指正。对知识点的描述以 Typeclassopedia 中所述为准。
导言
成为一位 Haskell 专家的关键:
- 理解 Haskell 中众多的类型。
- 熟悉众多例子,对 Haskell 中的每一个类型类以及彼此之间的关系构建起较深的直觉。
Typeclassopedia 为想要深入了解 Haskell 的人提供一个良好的起点,但读者需要经过不断地努力才可熟练掌握。
Haskell 的 type classes 结构示意图
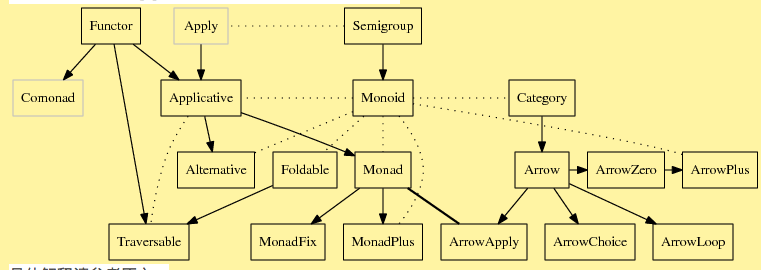
具体解释请参考原文。
Functor
Functor,即函子,是 Haskell 中普遍存在的、最基本的类型类。你可以用以下两种方式来理解 Functor:
- 它代表某种容器,该容器能够将某一函数应用到其每一个元素上。
- 它代表某种“可计算上下文”(computational context)。
我们试着分别用以上两种方法来理解列表:
- 列表是一种容器。通过 map,我们可以将一函数 f 应用到其每一个元素上。
- 列表代表一种未确定(non-deterministic)上下文——你可以其视为一个单一值,只是该值目前尚未从其可能的值(即该列表的所有元素)中选择出来。
同样,Maybe 也可以用两种方式来理解:
- Maybe 是一种能够容纳一个元素(Just a)或没有元素(Nothing)的容器。
- Maybe 代表一种可能失败的上下文。
总结而言,第一种方式更加具体和易于理解,然而缺乏普遍性。第二种方式通用性更强,但因其抽象性,可能需要一定的时间来理解。
即便如此,依然会存在某些 Functor 用以上两种途径都难以描述。因此理解 Functor 不能单纯通过类推,而是需要依靠理解其定义、阅读大量例子来获得准确的印象。
定义
Functor 定义如下:
class Functor f where
fmap :: (a -> b) -> f a -> f b
由 f a 和 f b 我们可知,f 不是类型,而是类型构造器(type constructor),即 f 应接受另一类型作为参数并返回一个具体的类型(更精准的表达则是 f 的 kind 必须是 * -> *)。
显然是可行的,但 则错误(因为 )。
实例
上文提到的 List 和 Maybe 的 Functor 实例(instances):
instance Functor [] where
fmap _ [] = []
fmap g (x:xs) = g x : fmap g xs
-- 或者可以直接 fmap = map
instance Functor Maybe where
fmap _ Nothing = Nothing
fmap g (Just a) = Just (g a)
下面再列举一些 Functor:
原文里提到的Control.Monad.Instances 在新的版本里已被移除,这些都已作为基础设施被默认实现。
- Either e 代表可以包含两种类型元素任意之一的容器(Right 或 Left e)。它和 Maybe 较为类似,两者都可以表示不能正常获得值时的错误,但 Either e 可以保存错误的额外信息。
- ((,) e) 代表可容纳一个元素、以及对该元素的某种注释信息的容器(本质上是类型为 (e, a) 的二元组)。将其写法转换为 (e,) 更易理解(考虑类比 (1+)),这样的类型声明语法需要开启扩展 TupleSections 才可通过编译。
- ((->) e),即可接受一个类型为 e 的值作为参数的函数类型,同样也是一个 Functor。以容器的观点看,它表示一个(可能无限元素的)容器,元素类型为 a,获取元素的索引的类型为 e。更有用的方式是将其理解为一个能够以类型为 e 的值、以只读方式来查询的上下文。这也是 ((->) e) 有时被称作 read monad 的原因(详细内容将在之后讲解)。
- IO 是一种 Functor,代表可以产生出类型为 a 的值的计算,该过程中可能伴随 I/O effects(或称 side effects,副作用)。
- 除此之外,其他许多容器库中的标准类型(比如 Tree、Map 和 Sequence)都是 Functor。为数不多的反例为 Set。
Typeclassopedia 法则
已经被作为 Functor 的 instance 的类型不一定就是一个 Functor。每一个有意义的 Functor 必须遵守以下 Functor 法则:
fmap id = id
fmap (g . h) = (fmap g) . (fmap h)
- 1
- 2
该法则的目的是为了确保 fmap 函数在应用到 Functor 时不会改变该 Functor 容器的结构——或者说不会改变 Functor 的上下文。
某些通过编译器检查的 Functor instance 也可能是无效的 Functor,比如:
-- Evil Functor instance
instance Functor [] where
fmap _ [] = []
fmap g (x:xs) = g x : g x : fmap g xs
如此会导致 Functor 在大量情境下丧失其正确的语义,因此必须小心避免。
Functor 有一些很有意思的特征:
- 每一个类型至多有一个与其对应的 Functor instance(且已通过 free theorem 的证明)。
- GHC 能够为许多类型自动创建出正确的 Functor。
- 任何满足第一条 Functor 法则的类型一定满足第二条法则(在不考虑 seq 和 undefined 的前提下)。
理解
你可以用两种方式来理解 fmap。第一种方式已经提到过了:传入两个参数,一个函数和一个容器,将这个函数应用到该容器所有的元素中,提供一个新的容器——或者说将一个函数应用到该 Functor 的上下文中的值,且不改变该 Functor 的上下文。
因为 Haskell 中的函数都是科里化的(curried),fmap 的类型可写为 fmap :: (a -> b) -> (f a -> f b)。以这种形式,我们还可以将 fmap 的作用理解为转换一个普通的函数到一个可以操作容器/内容的函数 (fmap g :: f a -> f b)。这一过程被称为“提升”(lift),即将一个函数从“普通的世界”提升到“f 类型的世界”。
https://blog.csdn.net/sinat_25226993/article/details/44063429