一些应该记住的东西(持续更新？再也不会更新了)

没什么用的目录

1.积性函数与杜教筛

2.搜索的几种优化与考试期望得分

3.乱讲

4.模拟退火系列

5.生成函数系列

2018.1.18

首先写写数学方面的吧(因为现在在学)……毕竟这里面的公式浩如烟海……

对着表推了十分钟愣是没发现……明明上午还证明过……

还有就是通过算贡献化简一些东西：

可以通过换元成d的倍数来证。

以及上面那对的第一个式子可以变换成

有了这个就好杜教筛了对吧……

第二个有时也可以构造成杜教筛……

2018.1.19

杜教筛的套路：求g(i)的前缀和G(i)，可以构造

其中f(i)和h(i)都是比较好求前缀和的函数，比如id(i)=i，id²(i)=i²，或者别的

然后求f(i)的前缀和：

即

于是就有

把右边的h(1)·G(n)提出来，就变成了：

因为之前说过f和h应该都是很好算前缀和的函数，比如i^2，比如[i==1]等。

预处理出G的前n^2/3项，然后哈希+记忆化搜索爆算即可。

 2018.1.26

说起来最近考的几场试里面有几题的暴力得分是这样的：

如果你写一个裸的搜索，你将获得10分。

如果你加上最优性剪枝、估价函数等一系列手段，你将获得20分？？

如果你再加上卡时这个东西，你将获得30分？？？

这都是些什么玩意儿……

话说回来，我在联赛之前看见过这么一套理论并且好像还是对的：

在有最优性剪枝的搜索(找最小值)中，应该把大的先拿去搜索，因为这样更快剪枝。

这又是个什么玩意儿……

反正考场上看见搜索题，要顺着下面的思路想：

优秀的估价函数>不优秀的估价函数>可行性剪枝>最优性剪枝>搜索顺序剪枝。

没错估价函数就是这么神奇……

2018.2.2

[OI无关][pkuwc血的教训]

网站上在动的时间并不一定是准的……隔一会刷新一次你会发现你的几分钟没了(-1s)

特别是某ku的百练，可以1个小时差4分钟……

下考我一脸懵逼看着旁边小哥，旁边的小哥：“确实已经6点半了呀”也是一脸懵逼看着我。

这都是些什么东西吧……

2018.2.9

模拟退火系列

精髓思想：温度越高，越不稳定，越容易发生跃动。

写一个接受函数判断，p=nowans-lastans：

inline bool Access(double p,double temp){
  if(p<=0)return true;
  return rand()<exp(-p/temp)*RAND_MAX;
}

具体而言，如果p<0，即当前答案比之前答案小，肯定接受。

如果p>0，exp(x)计算的是e的x次方，图像是这样的：

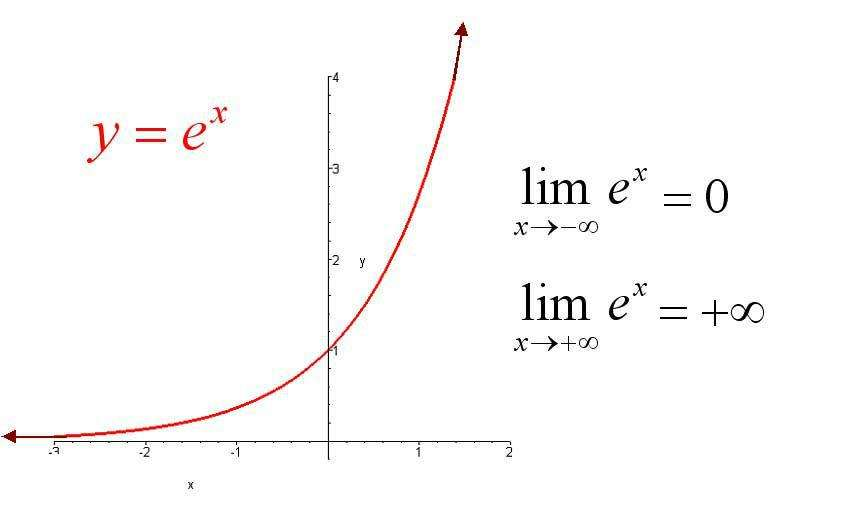
在x<0时返回一个(0,1)的实数。

p>0，当p越大，此时跃动越亏，(-p/temp)越小，exp越小。

当temp越小，(-p/temp)越小，exp越小。

是一种很合理的接受判断。

网上还有什么rand()%初始温度<当前温度就跃动之类的

都没有很好地利用p和temp两个量。

本来式子是这样的，两边都是0～1的实数：

因为除法常数太大，RAND_MAX移到右边去就可以了。

算法显然是非完美的，于是下面这一句话就很重要了：

模拟退火初温可以低，但一定要多烧。

实例：烧1000次，每次退10000下 = WA，烧10000次，每次退1000下=AC

也许烧出来的东西还是和初始状态关系很大吧……

然后就是退火时的判断。

因为温度很高时很不稳定，这个时候各种乱搞反而不容易进入正解。

于是可以掺一点贪心的东西进去，让p尽量<=0。

温度低了，稍微稳定了，这个时候常规退火效果可能更好。

比如说 BZOJ2428 均分数据 第一眼没人想的到退火

反倒很容易想到扔进和最小的组的贪心策略。

在温度大的时候用这个贪心可以提高正确率。

(事实上只要烧得够多(10086次选手)不用也能过)

2018.2.10再开一坑

生成函数/母函数系列

先引着几个东西：

(1)：广义组合数

一般组合数都是C(n,m)=n!/m!/(n-m)!，其中n,m均为非负整数且n>=m。

广义组合数也差不多，n可以是任意实数。

比如说C(-1.4,2)=(-1.4)*(-2.4)/2!=1.68。

于是引申开来这样的式子：

 

由此我们可以得出一个重要规律：

1/(1-x)^k (即(1-x)^-k)在xⁿ项的系数为C(n+k-1,n)。

稍作推广可得：

也可以写成

组合数上面的那个东西就不变了。

很多生成函数都会化到这种形式。

 

(2)：指数型母函数的两个重要等式

          

所以有这么个东西(要背的好多啊)

序列<1,1,1,1,1...>的指数型母函数是e^x

序列<1,-1,1,-1,1...>的指数型母函数是e^-x

然后再附赠两个：

序列<0,1,0,1,0...>的指数型母函数是(e^x-e^-x)/2

序列<1,0,1,0,1...>的指数型母函数是(e^x+e^-x)/2

好难记啊

放缩求导什么的……考场自己推吧……

 

2018年03月17日

感觉好久没碰博客园这个东西了……

看见网格图网络流想到黑白染色难道不是公理么？我这个××，×，×××。

 

好吧正事。 

(x,y)每次可以上下左右走的题目，可以转化为(x+y,x-y)。

这样，不管怎么走，横纵坐标都会改变，而且两维互不影响，就可以分开考虑了。

方案数也可以直接相乘什么的。

相当于坐标系旋转45°。

 

题面看见排列应该怎么想：

1.二分图，二分图上的连通块。

2.不用考虑重复元素的情况。

3.位置和值一一对应，从位置的改变映射到值的改变。

4.从小往大插入。

……

 

2018年04月07日之后

二阶差分(加一个等差)是可以只开一个数组的......

高斯消元……要判0……有些是自由元……(特别是异或消元！)

 

 

跟什么人说什么话，有些人的有些话不要听，有些话不要信，世界并非你心中一样真诚。