持续更新!!!
【例题】简单题(K-D tree)
线段树
【例题】(环上最大连续和) 给定一个长度为n的环形序列A,其中A1与A_n是相临的,现在有q次修改操作,每次操作会更改其中一个数,请对于每次修改输出修改后的最大连续和。
题目链接:POJ2750
【例题】给定一个长度为n的序列,可以修改任意个数字使其变成原来的相反数,求最小的逆序对数。
左偏树
【例题】派遣 题目链接
左偏树是一种具有左偏性质的堆有序二叉树(这里要注意,堆有序二叉树和二叉堆并不是同一种东西,因此左偏树并不是堆)。每一个节点存储的信息包括左右子节点、关键值以及距离(当然也有很多时候我们需要维护父节点)。
节点的距离可以这样定义:
某个节点被称为外节点,仅当这个节点的左子树或右子树为空。某一个节点的距离即该节点到与其最近的外节点经过的边数。易得,外节点的距离为0,空节点距离为−1。特别的,我们把根结点的距离称为这棵左偏树的距离。
这里有一张来自HolseLee dalao的图,以时空复杂度的角度来分析为什么左偏树是最常见的可并堆:
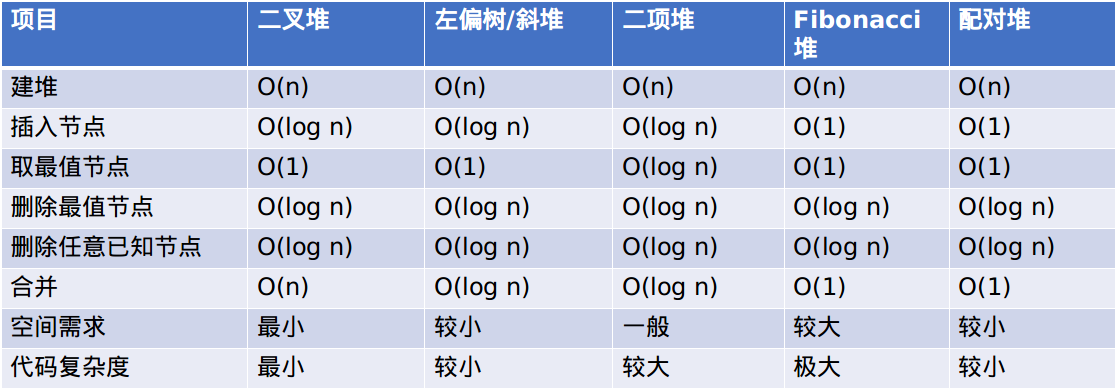
(imone dalao说,斜堆好写啊!)
至于时间复杂度为什么是这样的证明??没有的我不太会,此处挖坑待补吧。
三维偏序
【例题】给定三个长度为n的排列A,B,C,统计有多少对(i,j)满足(A_i<A_j,B_i<B_j,C_i<C_j)。其中(n<=5e6)。
解法:
我们先拆成二维偏序的问题。
设x为满足(A_i<A_j,B_i<B_j)的个数
y为满足(B_i<B_j,C_i<C_j)的个数
z为满足(C_i<C_j,A_i<A_j)的个数
显然会有结论:如果满足x,y,z这三种约束条件之二,就能满足题目中所要求的约束条件,我们称之为合法解。在计算这三个二维的时候,同一个合法解会被计算三次。
而不合法解只能被计算一次(因为如果有两次,根据上述所说,它就是合法解了)
我们设这个合法解的数量为c,那么根据排列组合原理,不合法解的数量为(C_n^2-c)。
所以我们有(x+y+z=3c+C_n^2-c)
所以(c=frac{1}{2}(x+y+z+C_n^2))
点分治
边分治
如果被菊花图卡了怎么办?加虚点。(只要保证和原图等价即可——点与点之间的边数和原先的一样)
你不知道怎么加虚点?上网搜啊。
【例题】BZOJ2870
????边分治到底是个什么啊?有用吗?有用吗?
链分治
整体二分
使用整体二分的题需要满足以下性质:
- 询问的答案具有可二分性
- 修改对询问的贡献是独立的,相互之间并不影响
- 不同的修改的贡献可以叠加
- 必须离线
顾名思义,就是对所有的询问一起二分。通常而言,这类题的询问是似乎于第几次修改之后满足条件。
莫队
推荐博客:胡小兔良心莫队教程
适用范围:
如果知道区间[l,r]的答案可以快速算出[l,r+1],[l,r-1],[l+1,r],[l-1,r]的答案的题目。
先将序列分成(sqrt n)分块,然后将所有询问做双关键字排序,第一关键字为询问的左端点所在的块,第二关键字为询问的右端点。那么两个询问[l1,r1],[l2,r2]之间转移的时间为(|l1-l2|+(r1-r2|)*t,其中t为转移一次的复杂度。
证明:
对于左端点,在同一块内的转移,一次不超过(sqrt n),在不同块之间的转移不超过(sqrt n)次。
右端点类似。总共的转移次数为(O(nsqrt n))级别的。
模板专用分割线
- 支持加减乘操作的线段树
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define MAXN 100010
using namespace std;
int n,m,mod;
int a[MAXN];
struct Node{int l,r,add,mul,sum;}t[MAXN<<2];
inline int ls(int x){return x<<1;}
inline int rs(int x){return x<<1|1;}
inline void push_up(int x){t[x].sum=(t[ls(x)].sum+t[rs(x)].sum)%mod;}
inline void f_mul(int x,int mul,int add)
{
int l=t[x].l,r=t[x].r;
t[x].sum=(1ll*t[x].sum*mul%mod+1ll*(r-l+1)*add%mod)%mod;
t[x].mul=(1ll*t[x].mul*mul)%mod;
t[x].add=(1ll*t[x].add*mul%mod+add)%mod;
}
inline void push_down(int x)
{
if(t[x].mul!=1||t[x].add)
{
f_mul(ls(x),t[x].mul,t[x].add);
f_mul(rs(x),t[x].mul,t[x].add);
t[x].mul=1;
t[x].add=0;
}
}
inline void build(int x,int l,int r)
{
t[x].l=l,t[x].r=r;
t[x].add=0,t[x].mul=1;
if(l==r) {t[x].sum=a[l]%mod;return;}
int mid=(l+r)>>1;
build(ls(x),l,mid);
build(rs(x),mid+1,r);
push_up(x);
}
inline void update_add(int x,int ll,int rr,int k)
{
int l=t[x].l,r=t[x].r;
if(ll<=l&&r<=rr)
{
t[x].sum=(t[x].sum+k*(r-l+1))%mod;
t[x].add=(t[x].add+k)%mod;
return;
}
push_down(x);
int mid=(l+r)>>1;
if(ll<=mid) update_add(ls(x),ll,rr,k);
if(mid<rr) update_add(rs(x),ll,rr,k);
push_up(x);
}
inline void update_mul(int x,int ll,int rr,int k)
{
int l=t[x].l,r=t[x].r;
if(ll<=l&&r<=rr)
{
t[x].sum=(1ll*t[x].sum*k)%mod;
t[x].mul=(1ll*t[x].mul*k)%mod;
t[x].add=(1ll*t[x].add*k)%mod;
return;
}
push_down(x);
int mid=(l+r)>>1;
if(ll<=mid) update_mul(ls(x),ll,rr,k);
if(mid<rr) update_mul(rs(x),ll,rr,k);
push_up(x);
}
inline int query(int x,int ll,int rr)
{
int l=t[x].l,r=t[x].r;
if(ll<=l&&r<=rr) return t[x].sum%mod;
push_down(x);
int mid=(l+r)>>1;
int cur_ans=0;
if(ll<=mid) cur_ans=(cur_ans+query(ls(x),ll,rr));
if(mid<rr) cur_ans=(cur_ans+query(rs(x),ll,rr));
return cur_ans%mod;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("ce.in","r",stdin);
#endif
scanf("%d%d%d",&n,&m,&mod);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
build(1,1,n);
for(int i=1;i<=m;i++)
{
int op,x,y,k;
scanf("%d",&op);
if(op==1)
{
scanf("%d%d%d",&x,&y,&k);
update_mul(1,x,y,k);
}
else if(op==2)
{
scanf("%d%d%d",&x,&y,&k);
update_add(1,x,y,k);
}
else
{
scanf("%d%d",&x,&y);
printf("%d
",query(1,x,y));
}
}
return 0;
}