一、题目:
n给定一个十进制的正整数,写下从1开始,到N的所有整数,然后数一下其中出现“1”的个数。
n要求:
n写一个函数 f(N) ,返回1 到 N 之间出现的 “1”的个数。例如 f(12) = 5。
n在32位整数范围内,满足条件的“f(N) =N”的最大的N是多少。
二、解题思路:
无。
三、程序源码:
import java.util.*; public class main { public static void main(String[] args) { // TODO Auto-generated method stub int num; Scanner S=new Scanner(System.in); System.out.print("请输入数字:"); num=S.nextInt(); System.out.print(num+"中出现数字1的个数为:"); System.out.println(Count(num)); for(int i=32767;i>0;i++) { if(Count(i)==i) { System.out.print("满足条件的“f(N) =N”的最大的N是"+i); break; } } } static int Count(int n) { int count=0; int factor=1; int LowerNum=0; int CurNum=0; int HigherNum=0; while (n/factor!=0) { LowerNum=n-(n/factor)*factor; CurNum=(n/factor)%10; HigherNum=n/(factor*10); switch (CurNum) { case 0: count=count+HigherNum*factor; break; case 1: count=count+HigherNum*factor + LowerNum +1; break; default: count=count+(HigherNum+1)*factor; break; } factor=factor*10; } return count; } }
四、程序运行截图: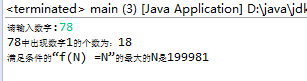
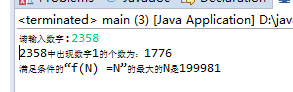
五、个人总结:
这次程序自己首先想到的是把1—N的每个数里边的1数一遍。但这不是最有效的办法,自己想的方法又实现不出来,在网上找了好多资料,只有上面的这种方法自己可以理解,因此就抄袭了下来。这个程序是根据如下规律写出来的:
1.一位十进制数:当N>=1时,f(N)=1;当N=0时,f(N)= 0;
2.两位十进制数:f(13)=个位出现1的个数+十位出现1的个数=2+4=6;
f(23)=个位出现1的个数+十位出现1的个数=3+10=13;
......
f(93)=个位出现1的个数+十位出现1的个数=10+10=20;
3.三位十进制数:f(123)=个位出现1的个数+十位出现1的个数+百位出现1的个数=13+20+24=57;
4.f(abcde),计算c位上的1的个数,需要看ab、c、de的情况:
当c=0时,受高位影响,百位上出现1的个数为:(ab)*100
当c=1时,受高位和低位影响,百位上出现1的个数为:(ab)*100+((cde)+1)
当c>1时,受高位影响,百位上出现1的个数为:((ab)+1)*100
自己理解的不是很到位,但是可以明白基本的意思,对自己无语。