bzoj 1005 [HNOI2008] 明明的烦恼 (prufer编码)

[HNOI2008]明明的烦恼

Time Limit: 1 Sec Memory Limit: 162 MB
Submit: 5907 Solved: 2305
[Submit][Status][Discuss]

Description

　　自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?

Input

　　第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1

Output

　　一个整数,表示不同的满足要求的树的个数,无解输出0

Sample Input

3
1
-1
-1

Sample Output

HINT

　　两棵树分别为1-2-3;1-3-2

题解：

　　　　prufer编码对于n个节点的数，是有n-2个数字的，不同的排列对应着不同的

　　　　树，一个度为x的点，出现在prufer编码中的次数是x-1。

　　　　所有就可以组合数学来解决这个问题。

假设度数有限制的点的数量为 cnt，他们的度数分别为：d[i]

另：

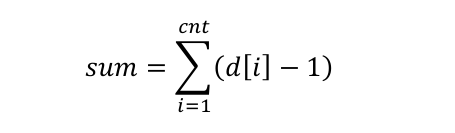
那么，在 Purfer Sequence 中的不同排列的总数为：

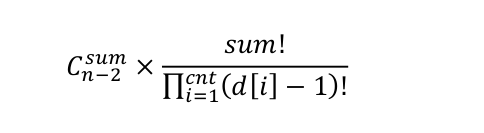
而剩下的 n-2-sum 个位置，可以随意的排列剩余的 n-cnt 个点，于是，总的方案数就应该是：

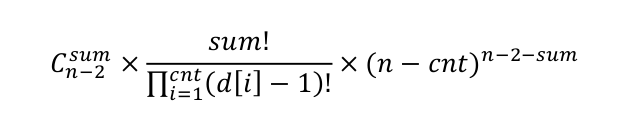
化简之后为：

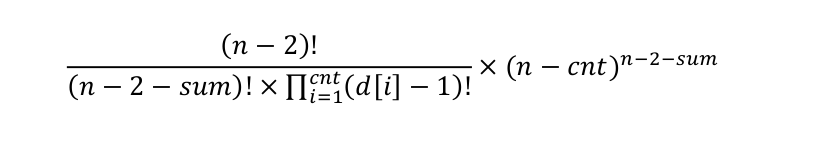
算了我在说一下，最后那个就是说，给了n-2-sum个位置，可以随便填数，填什么表示这个位置属于谁，好理解吧。

在有解的情况下，计算该结果输出就行了

无解的情况，就比如说超出了个数，这样子的，判断一下，根据prufer性质。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 int d[1005];
 4 struct bigint
 5 {
 6     int a[7000], len;
 7 
 8     bigint()
 9     {
10         memset(a, 0, 28000), len = 1;
11     }
12 
13     bigint operator* (const int &rhs) const
14     {
15         bigint ans;
16         ans.len = len + 6;
17         for(int i = 1; i <= len; ++i)
18             ans.a[i] += a[i] * rhs;
19         for(int i = 1; i < ans.len; ++i)
20             if(ans.a[i] > 9)
21             {
22                 ans.a[i + 1] += ans.a[i] / 10;
23                 ans.a[i] %= 10;
24             }
25         while(!ans.a[--ans.len]);
26         return ans;
27     }
28 
29     bigint operator/ (const int &rhs) const
30     {
31         bigint ans;
32         ans = *this, ++ans.len;
33         for(int i = ans.len; i; --i)
34         {
35             ans.a[i - 1] += ans.a[i] % rhs * 10;
36             ans.a[i] /= rhs;
37         }
38         while(!ans.a[--ans.len]);
39         return ans;
40     }
41 };
42 
43 int main()
44 {
45     int n, sum = 0, cnt = 0;
46     bigint ans;
47     scanf("%d", &n);
48     for(int i = 1; i <= n; ++i)
49     {
50         scanf("%d", d + i);
51         if(!d[i])
52         {
53             puts("0");
54             return 0;
55         }
56         if(~d[i]) ++cnt, sum += d[i] - 1;
57     }
58     if(sum > 2 * n - 2)
59     {
60         puts("0");
61         return 0;
62     }
63     ans.a[1] = 1;
64     for(int i = n - 1 - sum; i < n - 1; ++i)
65         ans = ans * i;
66     for(int i = 1; i <= n - 2 - sum; ++i)
67         ans = ans * (n - cnt);
68     for(int i = 1; i <= n; ++i)
69         for(int j = 2; j <= d[i] - 1; ++j)
70             ans = ans / j;
71     for(int i = ans.len; i; --i)
72         printf("%d", ans.a[i]);
73     puts("");
74 }

View Code