T1
题目还是比较难的，第一题就是第二类斯特林数的应用
就是对于几次的各项系数的问题，然后转化，然后发现第二步到
第三步是等价的，然后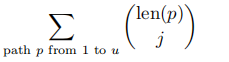
可以O（1）转移，就是nk得到，前面的再最后乘上去即可。
1 #include<cstring> 2 #include<iostream> 3 #include<algorithm> 4 #include<cmath> 5 #include<cstdio> 6 #include<queue> 7 8 #define mod 998244353 9 #define N 100007 10 #define M 200007 11 #define K 507 12 #define ll long long 13 using namespace std; 14 inline int read() 15 { 16 int x=0;char ch=getchar(); 17 while(ch<'0'||ch>'9')ch=getchar(); 18 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} 19 return x; 20 } 21 22 int n,m,k; 23 int cnt,hed[N],rea[M],nxt[M]; 24 int du[N],fz[N],f[N][K],s2[N][K]; 25 queue<int>q; 26 27 void add(int u,int v) 28 { 29 nxt[++cnt]=hed[u]; 30 hed[u]=cnt; 31 rea[cnt]=v; 32 } 33 int main() 34 { 35 memset(hed,-1,sizeof(hed)); 36 n=read(),m=read(),k=read(); 37 for (int i=1;i<=m;i++) 38 { 39 int x=read(),y=read(); 40 add(x,y),du[y]++; 41 } 42 fz[0]=1; 43 for (int i=1;i<=k;i++) 44 fz[i]=(ll)fz[i-1]*i%mod; 45 s2[0][0]=1; 46 for (int i=1;i<=k;i++) 47 for (int j=1;j<=i;j++) 48 s2[i][j]=((ll)s2[i-1][j]*j+s2[i-1][j-1])%mod; 49 f[1][0]=1,q.push(1); 50 while(!q.empty()) 51 { 52 int u=q.front();q.pop(); 53 for (int i=hed[u];i!=-1;i=nxt[i]) 54 { 55 int v=rea[i]; 56 f[v][0]=(f[v][0]+f[u][0])%mod; 57 for (int j=1;j<=k;j++) 58 f[v][j]=((ll)f[v][j]+f[u][j-1]+f[u][j])%mod; 59 if(--du[v]==0)q.push(v); 60 } 61 } 62 for (int i=1;i<=n;i++) 63 { 64 int ans=0; 65 for (int j=0;j<=k;j++) 66 ans=((ll)ans+(ll)s2[k][j]*fz[j]%mod*f[i][j])%mod; 67 printf("%d ",ans); 68 } 69 }
T2
这道题目我们先看如果没有限制范围，
这里题解中一种方法，在自己的点先加上一，然后与其相邻的dfs序的同色点的lca-1
什么意思，可以想象是合并的意思，就是对于图中左子树，lca为什么减1，就是左子树中
左右对于答案统计重复了，然后合并完以后为什么可以直接相邻，因为不是其子树的，
那么lca必定比其lca上面，可以代替其lca的左右，然后就好了。
1 #include<cstring> 2 #include<cmath> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstdio> 6 #include<set> 7 #include<vector> 8 9 #define N 100007 10 #define fzy pair<int,int> 11 #define zz set<fzy>::iterator 12 using namespace std; 13 inline int read() 14 { 15 int x=0,f=1;char ch=getchar(); 16 while(ch<'0'||ch>'9'){if (ch=='-')f=-1;ch=getchar();} 17 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} 18 return x*f; 19 } 20 21 int n,q,type,tim,sz; 22 int cnt,hed[N],nxt[N*2],rea[N*2]; 23 int col[N],in[N],out[N]; 24 int dep[N],fa[N][19]; 25 int root[N*4],tr[N*400],ls[N*400],rs[N*400]; 26 vector<int>col_vec[N]; 27 set<fzy>st[N]; 28 29 void dfs(int u,int f) 30 { 31 in[u]=++tim; 32 for (int i=1;(1<<i)<=dep[u];i++)fa[u][i]=fa[fa[u][i-1]][i-1]; 33 for (int i=hed[u];i!=-1;i=nxt[i]) 34 { 35 int v=rea[i]; 36 if (v==f)continue; 37 fa[v][0]=u,dep[v]=dep[u]+1,dfs(v,u); 38 } 39 out[u]=tim; 40 } 41 int lca(int a,int b) 42 { 43 if (dep[a]<dep[b])swap(a,b); 44 int i;for (i=0;(1<<i)<=dep[a];i++);i--; 45 for (int j=i;j>=0;j--) 46 if (dep[a]-(1<<j)>=dep[b])a=fa[a][j]; 47 if (a==b) return a; 48 for (int j=i;j>=0;j--) 49 if (fa[a][j]!=fa[b][j])a=fa[a][j],b=fa[b][j]; 50 return fa[a][0]; 51 } 52 void add(int u,int v) 53 { 54 nxt[++cnt]=hed[u]; 55 hed[u]=cnt; 56 rea[cnt]=v; 57 } 58 bool cmp(int x,int y) 59 { 60 return in[x]<in[y]; 61 } 62 int query_sc(int p,int l,int r,int x,int y) 63 { 64 if (l==x&&y==r)return tr[p]; 65 int mid=(l+r)>>1; 66 if (y<=mid) return query_sc(ls[p],l,mid,x,y); 67 else if (x>mid) return query_sc(rs[p],mid+1,r,x,y); 68 else return query_sc(ls[p],l,mid,x,mid)+query_sc(rs[p],mid+1,r,mid+1,y); 69 } 70 int query_fr(int p,int l,int r,int x,int y,int clo_x,int clo_y) 71 { 72 if (l==x&&y==r)return query_sc(root[p],1,n,clo_x,clo_y); 73 int mid=(l+r)>>1; 74 if (y<=mid) return query_fr(p<<1,l,mid,x,y,clo_x,clo_y); 75 else if (x>mid) return query_fr(p<<1|1,mid+1,r,x,y,clo_x,clo_y); 76 else return query_fr(p<<1,l,mid,x,mid,clo_x,clo_y)+query_fr(p<<1|1,mid+1,r,mid+1,y,clo_x,clo_y); 77 } 78 void ins_sc(int &p,int l,int r,int x,int z) 79 { 80 if (!p)p=++sz; 81 // cout<<p<<" "<<l<<" "<<r<<" "<<endl; 82 tr[p]+=z; 83 if (l==r) return; 84 int mid=(l+r)>>1; 85 if (x<=mid) ins_sc(ls[p],l,mid,x,z); 86 else ins_sc(rs[p],mid+1,r,x,z); 87 } 88 void ins_fr(int p,int l,int r,int x,int y,int z) 89 { 90 ins_sc(root[p],1,n,y,z); 91 // cout<<" hhhhhh"<<p<<" "<<l<<" "<<r<<" "<<x<<endl; 92 if (l==r) return; 93 int mid=(l+r)>>1; 94 if (x<=mid)ins_fr(p<<1,l,mid,x,y,z); 95 else ins_fr(p<<1|1,mid+1,r,x,y,z); 96 } 97 void init() 98 { 99 for (int i=1;i<=n;i++) 100 { 101 sort(col_vec[i].begin(),col_vec[i].end(),cmp); 102 for (int j=0;j<col_vec[i].size();j++) 103 { 104 if (j) ins_fr(1,1,n,in[lca(col_vec[i][j],col_vec[i][j-1])],i,-1); 105 // cout<<"zhi="<<in[col_vec[i][j]]<<endl; 106 ins_fr(1,1,n,in[col_vec[i][j]],i,1); 107 st[i].insert(make_pair(in[col_vec[i][j]],col_vec[i][j])); 108 } 109 } 110 } 111 int main() 112 { 113 memset(hed,-1,sizeof(hed)); 114 n=read(),q=read(),type=read(); 115 for (int i=1;i<=n;i++) 116 { 117 col[i]=read(); 118 col_vec[col[i]].push_back(i); 119 } 120 for (int i=1;i<n;i++) 121 { 122 int x=read(),y=read(); 123 add(x,y),add(y,x); 124 } 125 dep[1]=1,dfs(1,0); 126 init(); 127 int lastans=0; 128 while(q--) 129 { 130 int flag=read(); 131 if (flag==1) 132 { 133 int u=read(),l=read(),r=read(); 134 if (type)u^=lastans,l^=lastans,r^=lastans; 135 printf("%d ",lastans=query_fr(1,1,n,in[u],out[u],l,r)); 136 } 137 else 138 { 139 int u=read(),y=read(); 140 if (type)u^=lastans,y^=lastans; 141 //---------------------------erase-begin------------------------------------------------------- 142 zz it=st[col[u]].lower_bound(make_pair(in[u],u)); 143 if (it!=st[col[u]].begin()) 144 { 145 zz front=it; 146 front--; 147 ins_fr(1,1,n,in[lca((*front).second,u)],col[u],1); 148 } 149 zz tl=it;tl++; 150 if (tl!=st[col[u]].end()) ins_fr(1,1,n,in[lca((*tl).second,u)],col[u],1); 151 if(it!=st[col[u]].begin()&&tl!=st[col[u]].end()) 152 { 153 zz hd=it;hd--; 154 ins_fr(1,1,n,in[lca(((*hd).second),(*tl).second)],col[u],-1); 155 } 156 ins_fr(1,1,n,in[u],col[u],-1); 157 st[col[u]].erase(it); 158 //---------------------------erase-end--------------------------------------------------------- 159 col[u]=y; 160 //---------------------------insert-begin----------------------------------------------------- 161 st[col[u]].insert(make_pair(in[u],u)); 162 it=st[col[u]].lower_bound(make_pair(in[u],u)); 163 if (it!=st[col[u]].begin()) 164 { 165 zz front=it;front--; 166 ins_fr(1,1,n,in[lca((*front).second,u)],col[u],-1); 167 } 168 tl=it;tl++; 169 if (tl!=st[col[u]].end()) ins_fr(1,1,n,in[lca((*tl).second,u)],col[u],-1); 170 if(it!=st[col[u]].begin()&&tl!=st[col[u]].end()) 171 { 172 zz front=it;front--; 173 ins_fr(1,1,n,in[lca((*front).second,(*tl).second)],col[u],1); 174 } 175 ins_fr(1,1,n,in[u],col[u],1); 176 } 177 } 178 }
T3
题目意思就是随机点分治，任选一个点为重心，然后各子树中任选一个点作为下一层点分树的点，
然后问题转换就是显然的，在原树中两个点之间绝对有一个属于点分的点，所以两个编号相同点之间
一定存在一个属于点分树上层的点，即编号比它们小的点。
然后题解又引出概念，不覆盖的意思是对于u，
(也就是说对于k ∈ S, 存在一个点 v 满足 labelv = k 并且 v 到 u 的路径上的每个点的 label 都 ≥ k)
如果那一位没被覆盖，就为1，覆盖了就为0
为什么前面的位置任意，因为，随意的是否覆盖，对于当前位置都是>k的
为什么k位上一定为0呢，假设没被覆盖，
那么假设B是k，然后B没被覆盖，那么A-B中必有一个label<k，则与假设矛盾，
必其小的为什么不能同时为1
假设A,B上lable相同，C是比A,B小的，那么就不满足两个编号相同的点之间有一个比其小的点，
所以可以解释了。
最后这样的话n个点，k是枚举的编号，然后4^k的意思是每位上有0,0 0,1 1,0 1,1 四种情况
然后发现比k大的可以前缀和维护，比k小的只有三种情况了，不可能同时为一，
所以复杂度O(nk3^k)
先枚举k
1 #include<cstring> 2 #include<cmath> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstdio> 6 7 #define ll long long 8 #define N 52 9 #define mod 998244353 10 using namespace std; 11 inline int read() 12 { 13 int x=0,f=1;char ch=getchar(); 14 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 15 while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} 16 return x*f; 17 } 18 19 int n,k; 20 int cnt,hed[N],nxt[N*2],rea[N*2],f[N][(1<<15)+7]; 21 int q[N],fa[N]; 22 23 void add(int u,int v) 24 { 25 nxt[++cnt]=hed[u]; 26 hed[u]=cnt; 27 rea[cnt]=v; 28 } 29 inline void modify(int &x,int y) 30 { 31 x=x+y<mod?x+y:x+y-mod; 32 } 33 int main() 34 { 35 memset(hed,-1,sizeof(hed)); 36 n=read(),k=read(); 37 for (int i=1,x,y;i<n;i++) 38 { 39 x=read(),y=read(); 40 add(x,y),add(y,x); 41 } 42 int hd=0,tl=1; 43 q[1]=1; 44 while(hd<tl) 45 { 46 hd++;int u=q[hd]; 47 for (int i=hed[q[hd]];i!=-1;i=nxt[i]) 48 { 49 int v=rea[i]; 50 if (v!=fa[u])fa[q[++tl]=v]=u; 51 } 52 } 53 for (int i=n;i>=1;i--) 54 { 55 int u=q[i]; 56 for (int j=0;j<k;j++) 57 { 58 int *F=f[u]+(1<<j); 59 F[0]=1; 60 for (int e=hed[u];e!=-1;e=nxt[e]) 61 { 62 int v=rea[e]; 63 if (v==fa[u])continue; 64 static int S[1<<15]; 65 for (int t=0;t<1<<j;t++) 66 S[t]=0; 67 for (int t=0;t<1<<k;t+=2<<j) 68 for (int l=0;l<1<<j;l++) 69 modify(S[l],f[v][t+l]); 70 static int G[1<<15]; 71 for (int t=0;t<1<<j;t++) 72 G[t]=0; 73 for (int t=0;t<1<<j;t++) 74 for (int l=t;l<1<<j;l=l+1|t) 75 G[l]=(G[l]+(ll)F[t]*S[l-t])%mod; 76 for (int t=0;t<1<<j;t++) 77 F[t]=G[t]; 78 } 79 } 80 } 81 int ans=0; 82 for (int i=0;i<1<<k;i++) 83 modify(ans,f[1][i]); 84 printf("%d ",ans); 85 }
先枚举子节点
1 int n,k,cnt,head[55],Next[105],vet[105],f[55][(1<<15)]; 2 int q[55],fa[55],G[(1<<15)],S[(1<<15)]; 3 void add(int x,int y){ 4 vet[++cnt]=y; 5 Next[cnt]=head[x]; 6 head[x]=cnt; 7 } 8 void modify(int &x,int y){ 9 x=x+y; 10 if (x>mod) x=x-mod; 11 } 12 int main(){ 13 n=read(),k=read(); 14 for (int i=1; i<n; i++){ 15 int x,y; 16 x=read(),y=read(); 17 add(x,y); 18 add(y,x); 19 } 20 int hd=0,tl=1; 21 q[0]=1; 22 while (hd<tl){ 23 int u=q[hd++]; 24 for (int i=head[u]; i; i=Next[i]){ 25 int v=vet[i]; 26 if (v==fa[u]) continue; 27 fa[v]=u; 28 q[tl++]=v; 29 } 30 } 31 for (int i=n-1; i>=0; i--){ 32 int u=q[i]; 33 for (int j=0; j<k; j++) f[u][(1<<j)]=1; 34 for (int e=head[u]; e; e=Next[e]){ 35 int v=vet[e]; 36 for (int j=0; j<k; j++){ 37 if (v==fa[u]) continue; 38 for (int t=0; t<(1<<j); t++) S[t]=0; 39 for (int t=0; t<(1<<k); t+=(1<<(j+1))) 40 for (int l=0; l<(1<<j); l++) 41 modify(S[l],f[v][t+l]); 42 for (int t=0; t<(1<<j); t++) G[t]=0; 43 for (int t=0; t<(1<<j); t++) 44 for (int l=t; l<(1<<j); l=(l+1)|t) 45 G[l]=(G[l]+(ll)f[u][(1<<j)+t]*S[l-t])%mod; 46 for (int t=0; t<(1<<j); t++) f[u][(1<<j)+t]=G[t]; 47 } 48 } 49 } 50 int ans=0; 51 for (int i=0; i<1<<k; i++) 52 modify(ans,f[1][i]); 53 printf("%d ",ans); 54 }