数据预测算法-指数平滑法-2

一次、二次、三次指数平滑计算思想及代码

概述

一般常用到的指数平滑法为一次指数平滑、二次指数平滑和三次指数平滑，高次指数平滑一般比较难见到，因此本文着重介绍了一次、二次和三次指数平滑的特点与不同。

一次指数平滑一般应用于直线型数据，且一次指数平滑具有滞后性，可以说明有明显的时间性、季节性。

二次指数平滑一般也应用于直线型，但是效果会比一次指数平滑好很多，也就相当于加强版的一次指数平滑。

三次指数平滑可以应用于抛物线型的数据，因为数据在二次平滑过后还是具有斜率，那么可以继续使用三次指数平滑。

初值：不管什么指数平滑都会有个初值，假如数据大于20项，那么初值就可以认定为第一个数据，或者利用下列公式计算也行；假如数据小于20项，则初始值为：

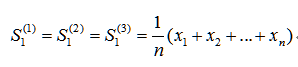
低于20项一般取3，大于20的看着取就行了。

一次指数平滑：

一次指数平滑需要滞后一期，给定平滑系数，那么一次指数平滑的计算公式为：

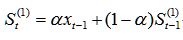
预测第期的数值则是上一期的实际值与预测值的加权平均，预测公式为：

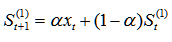
二次指数平滑：

给定平滑系数，那么二次指数平滑的计算公式为：

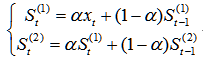
预测未来期的值的计算公式为：

其中：

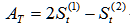
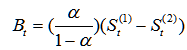
三次指数平滑：

给定平滑系数，那么三次指数平滑的计算公式为：

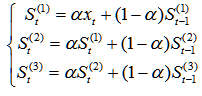
预测未来期的值的计算公式为：

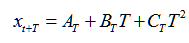
其中：

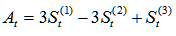
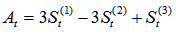
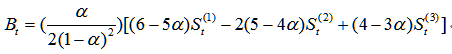
下面举例说明，数据如下：

253993	275396.2	315229.5	356949.6	400158.2	442431.7	495102.9	570164.8	640993.1	704250.4	767455.4	781807.8	776332.3	794161.7	834177.7	931651.5	1028390	1114914
133	88	150	123	404	107	674	403	243	257	900	1043	1156	895	1200	1038	1024	1283

引入均方误差概念来判断平滑系数是否准确：

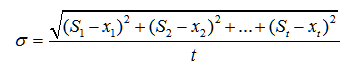
要使最小则构成了一个关于的函数，由此可以得到最优的平滑系数，这里可以引入线性规划的思想来求得最优解

但是：

python没有线性规划的包，所以就没有细致的代码写出来了，不过经过手动计算尝试这样子是可行的

python代码

一次指数平滑

在python3下编程，一次指数平滑代码为：

S1_1 = []
        for m in range(0, len(info_data_id)):
            S1_1_empty = []
            x = 0
            for n in range(0, 3):
                x = x + int(info_data_sales[m][n])
            x = x / 3
            S1_1_empty.append(x)
            S1_1.append(S1_1_empty)
        # print(S1_1)

        a = []  ##这是用来存放阿尔法的数组
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            v = input('请输入第' + str(i + 1) + '组数据的a：')
            a.append(v)

        for i in range(0, len(info_data_sales)):
            MSE = 0
            for j in range(0, len(info_data_sales[i])):
                S1_1[i].append(
                    float(a[i]) * int(info_data_sales[i][j]) + (1 - float(a[i])) * int(S1_1[i][j]))  ##计算预估值
                MSE = (int(S1_1[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE
                # print(info_data_sales[i][j], S1_1[i][j])
            MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i]))  ##得到均方误差
            info_MSE.append(MSE)
        # print(info_MSE)
        # print(S1_1)
        for i in range(0, len(S1_1)):
            print('第' + str(i + 1) + '组的一次平滑预估值为:' + str(S1_1[i][len(S1_1[i]) - 1]) + '；均方误差为：' + str(info_MSE[i]))

二次指数平滑代码

S2_1 = []
        S2_2 = []
        for m in range(0, len(info_data_id)):
            S2_1_empty = []
            x = 0
            for n in range(0, 3):
                x = x + float(info_data_sales[m][n])
            x = x / 3
            S2_1_empty.append(x)
            S2_1.append(S2_1_empty)
            S2_2.append(S2_1_empty)
        # print(S2_2)
        a = []  ##这是用来存放阿尔法的数组
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            v = float(input('请输入第' + str(i + 1) + '组数据的a：'))
            a.append(v)

        ##下面是计算一次指数平滑的值
        S2_1_new1 = []
        for i in range(0, len(info_data_sales)):
            S2_1_new = [[]] * len(info_data_id)
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S2_1_new[i].append(
                        float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(S2_1[i][j]))
                else:
                    S2_1_new[i].append(float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(
                        S2_1_new[i][j - 1]))  ##计算一次指数的值
            S2_1_new1.append(S2_1_new[i])
        # print(S2_1_new1)
        # print(len(S2_1_new1[i]))

        ##下面是计算二次指数平滑的值
        S2_2_new1 = []
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            S2_2_new = [[]] * len(info_data_id)
            MSE = 0
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S2_2_new[i].append(float(a[i]) * float(S2_1_new1[i][j]) + (1 - float(a[i])) * float(S2_2[i][j]))
                else:
                    S2_2_new[i].append(float(a[i]) * float(S2_1_new1[i][j]) + (1 - float(a[i])) * float(
                        S2_2_new[i][j - 1]))  ##计算二次指数的值
                MSE = (int(S2_2_new[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE
            MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i]))
            info_MSE.append(MSE)
            S2_2_new1.append(S2_2_new[i])
        # print(S2_2_new1)
        # print(len(S2_2_new1[i]))

        ##下面是计算At、Bt以及每个预估值Xt的值，直接计算预估值，不一一列举Xt的值了
        u = input('你要预估多少期？')
        Xt = []
        for i in range(0, len(info_data_sales)):
            At = (float(S2_1_new1[i][len(S2_1_new1[i]) - 1]) * 2 - float(S2_2_new1[i][len(S2_2_new1[i]) - 1]))
            Bt = (float(a[i]) / (1 - float(a[i])) * (
            float(S2_1_new1[i][len(S2_1_new1[i]) - 1]) - float(S2_2_new1[i][len(S2_2_new1[i]) - 1])))
            Xt.append(At + Bt * int(u))
            print('第' + str(i + 1) + '组的二次平滑预估值为:' + str(Xt[i]) + '；均方误差为：' + str(info_MSE[i]))

三次指数平滑

S3_1 = []
        S3_2 = []
        S3_3 = []
        for m in range(0, len(info_data_id)):
            S3_1_empty = []
            x = 0
            for n in range(0, 3):
                x = x + float(info_data_sales[m][n])
            x = x / 3
            S3_1_empty.append(x)
            S3_1.append(S3_1_empty)
            S3_2.append(S3_1_empty)
            S3_3.append(S3_1_empty)
        # print(S3_1)
        a = []  ##这是用来存放阿尔法的数组
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            v = float(input('请输入第' + str(i + 1) + '组数据的a：'))
            a.append(v)

        ##下面是计算一次指数平滑的值
        S3_1_new1 = []
        for i in range(0, len(info_data_sales)):
            S3_1_new = [[]] * len(info_data_id)
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S3_1_new[i].append(
                        float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(S3_1[i][j]))
                else:
                    S3_1_new[i].append(float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(
                        S3_1_new[i][j - 1]))  ##计算一次指数的值
            S3_1_new1.append(S3_1_new[i])

        ##下面是计算二次指数平滑的值
        S3_2_new1 = []
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            S3_2_new = [[]] * len(info_data_id)
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S3_2_new[i].append(float(a[i]) * float(S3_1_new1[i][j]) + (1 - float(a[i])) * float(S3_2[i][j]))
                else:
                    S3_2_new[i].append(float(a[i]) * float(S3_1_new1[i][j]) + (1 - float(a[i])) * float(
                        S3_2_new[i][j - 1]))  ##计算二次指数的值
            S3_2_new1.append(S3_2_new[i])

        ##下面是计算二次指数平滑的值
        S3_3_new1 = []
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            S3_3_new = [[]] * len(info_data_id)
            MSE = 0
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S3_3_new[i].append(float(a[i]) * float(S3_2_new1[i][j]) + (1 - float(a[i])) * float(S3_3[i][j]))
                else:
                    S3_3_new[i].append(float(a[i]) * float(S3_2_new1[i][j]) + (1 - float(a[i])) * float(
                        S3_3_new[i][j - 1]))  ##计算三次指数的值
                MSE = (int(S3_3_new[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE
            MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i]))
            info_MSE.append(MSE)
            S3_3_new1.append(S3_3_new[i])
            # print(S3_3_new1)

        ##下面是计算At、Bt、Ct以及每个预估值Xt的值，直接计算预估值，不一一列举Xt的值了
        u = input('你要预估多少期？')
        Xt = []
        for i in range(0, len(info_data_sales)):
            At = (
            float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) * 3 - float(S3_2_new1[i][len(S3_2_new1[i]) - 1]) * 3 + float(
                S3_3_new1[i][len(S3_3_new1[i]) - 1]))
            Bt = ((float(a[i]) / (2 * ((1 - float(a[i])) ** 2))) * ((6 - 5 * float(a[i])) * (
            float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) - 2 * (5 - 4 * float(a[i])) * float(
                S3_2_new1[i][len(S3_2_new1[i]) - 1]) + (4 - 3 * float(a[i])) * float(
                S3_3_new1[i][len(S3_3_new1[i]) - 1]))))
            Ct = (((float(a[i])) ** 2) / (2 * ((1 - float(a[i])) ** 2))) * (
            float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) - float(S3_2_new1[i][len(S3_2_new1[i]) - 1])*2 + float(
                S3_3_new1[i][len(S3_3_new1[i]) - 1]))
            Xt.append(At + Bt * int(u) + Ct * (int(u) ** 2))
            print('第' + str(i + 1) + '组的三次平滑预估值为:' + str(Xt[i]) + '；均方误差为：' + str(info_MSE[i]))

由于注释写得很清楚了，就不一段一段的解释了

明显看出数列为线性的数列，所以用二次指数平滑会更好

得到的二次平滑结果如下：

误差判断：

误差判断	预估值	实际值	误差
数列1	1193179	1192201	0.08%
数列2	1250	1371	9.68%

由此可见预测效果非常好

完整代码

 from openpyxl import load_workbook
import xlsxwriter

if __name__ == '__main__':
    judge = input('请选择使用几次指数平滑：一次请按1；二次请按2；三次请按3：')
    ##这里是打开excel将数据储存到数组里面
    wb = load_workbook(filename=r'C:UsersAdministratorDesktopdata.xlsx')  ##读取路径
    ws = wb.get_sheet_by_name("Sheet1")  ##读取名字为Sheet1的sheet表
    info_data_id = []
    info_data_sales = []

    for row_A in range(1, 3):  ## 遍历第1行到2行
        id = ws.cell(row=row_A, column=1).value  ## 遍历第1行到2行，第1列
        info_data_id.append(id)
    for row_num_BtoU in range(1, len(info_data_id) + 1):  ## 遍历第1行到2行
        row_empty = []  ##建立一个空数组作为临时储存地，每次换行就被清空
        for i in range(2, 20):  ## 遍历第1行到2行，第1到19列
            data = ws.cell(row=row_num_BtoU, column=i).value
            if data == None:
                pass
            else:
                row_empty.append(data)  ##将单元格信息储存进去
        info_data_sales.append(row_empty)  ##row_empty每次储存完1到19列后压给info_data_sales，然后row_empty被清空
    # print(info_data_id)
    # print(info_data_sales)
    if judge == '1':
        ##############################下面是计算St(1)下面写为S1_t_######################################
        print('你选择了一次指数平滑预测')
        ##一次指数平滑的初值为S1_1，用S1_1来储存每一组数据的一次平滑的数值
        S1_1 = []
        for m in range(0, len(info_data_id)):
            S1_1_empty = []
            x = 0
            for n in range(0, 3):
                x = x + int(info_data_sales[m][n])
            x = x / 3
            S1_1_empty.append(x)
            S1_1.append(S1_1_empty)
        # print(S1_1)

        a = []  ##这是用来存放阿尔法的数组
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            v = input('请输入第' + str(i + 1) + '组数据的a：')
            a.append(v)

        for i in range(0, len(info_data_sales)):
            MSE = 0
            for j in range(0, len(info_data_sales[i])):
                S1_1[i].append(
                    float(a[i]) * int(info_data_sales[i][j]) + (1 - float(a[i])) * int(S1_1[i][j]))  ##计算预估值
                MSE = (int(S1_1[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE
                # print(info_data_sales[i][j], S1_1[i][j])
            MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i]))  ##得到均方误差
            info_MSE.append(MSE)
        # print(info_MSE)
        # print(S1_1)
        for i in range(0, len(S1_1)):
            print('第' + str(i + 1) + '组的一次平滑预估值为:' + str(S1_1[i][len(S1_1[i]) - 1]) + '；均方误差为：' + str(info_MSE[i]))

    if judge == '2':
        ##############################下面是计算St(2)下面写为S2_t_######################################
        print('你选择了二次指数平滑预测')

        ##二次指数平滑的初值为S2_1，用S2_1_new来储存每一组数据的一次平滑的数值
        S2_1 = []
        S2_2 = []
        for m in range(0, len(info_data_id)):
            S2_1_empty = []
            x = 0
            for n in range(0, 3):
                x = x + float(info_data_sales[m][n])
            x = x / 3
            S2_1_empty.append(x)
            S2_1.append(S2_1_empty)
            S2_2.append(S2_1_empty)
        # print(S2_2)
        a = []  ##这是用来存放阿尔法的数组
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            v = float(input('请输入第' + str(i + 1) + '组数据的a：'))
            a.append(v)

        ##下面是计算一次指数平滑的值
        S2_1_new1 = []
        for i in range(0, len(info_data_sales)):
            S2_1_new = [[]] * len(info_data_id)
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S2_1_new[i].append(
                        float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(S2_1[i][j]))
                else:
                    S2_1_new[i].append(float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(
                        S2_1_new[i][j - 1]))  ##计算一次指数的值
            S2_1_new1.append(S2_1_new[i])
        # print(S2_1_new1)
        # print(len(S2_1_new1[i]))

        ##下面是计算二次指数平滑的值
        S2_2_new1 = []
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            S2_2_new = [[]] * len(info_data_id)
            MSE = 0
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S2_2_new[i].append(float(a[i]) * float(S2_1_new1[i][j]) + (1 - float(a[i])) * float(S2_2[i][j]))
                else:
                    S2_2_new[i].append(float(a[i]) * float(S2_1_new1[i][j]) + (1 - float(a[i])) * float(
                        S2_2_new[i][j - 1]))  ##计算二次指数的值
                MSE = (int(S2_2_new[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE
            MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i]))
            info_MSE.append(MSE)
            S2_2_new1.append(S2_2_new[i])
        # print(S2_2_new1)
        # print(len(S2_2_new1[i]))

        ##下面是计算At、Bt以及每个预估值Xt的值，直接计算预估值，不一一列举Xt的值了
        u = input('你要预估多少期？')
        Xt = []
        for i in range(0, len(info_data_sales)):
            At = (float(S2_1_new1[i][len(S2_1_new1[i]) - 1]) * 2 - float(S2_2_new1[i][len(S2_2_new1[i]) - 1]))
            Bt = (float(a[i]) / (1 - float(a[i])) * (
            float(S2_1_new1[i][len(S2_1_new1[i]) - 1]) - float(S2_2_new1[i][len(S2_2_new1[i]) - 1])))
            Xt.append(At + Bt * int(u))
            print('第' + str(i + 1) + '组的二次平滑预估值为:' + str(Xt[i]) + '；均方误差为：' + str(info_MSE[i]))

    if judge == '3':
        ##############################下面是计算St(3)下面写为S3_t_######################################
        print('你选择了三次指数平滑预测')
        S3_1 = []
        S3_2 = []
        S3_3 = []
        for m in range(0, len(info_data_id)):
            S3_1_empty = []
            x = 0
            for n in range(0, 3):
                x = x + float(info_data_sales[m][n])
            x = x / 3
            S3_1_empty.append(x)
            S3_1.append(S3_1_empty)
            S3_2.append(S3_1_empty)
            S3_3.append(S3_1_empty)
        # print(S3_1)
        a = []  ##这是用来存放阿尔法的数组
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            v = float(input('请输入第' + str(i + 1) + '组数据的a：'))
            a.append(v)

        ##下面是计算一次指数平滑的值
        S3_1_new1 = []
        for i in range(0, len(info_data_sales)):
            S3_1_new = [[]] * len(info_data_id)
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S3_1_new[i].append(
                        float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(S3_1[i][j]))
                else:
                    S3_1_new[i].append(float(a[i]) * float(info_data_sales[i][j]) + (1 - float(a[i])) * float(
                        S3_1_new[i][j - 1]))  ##计算一次指数的值
            S3_1_new1.append(S3_1_new[i])

        ##下面是计算二次指数平滑的值
        S3_2_new1 = []
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            S3_2_new = [[]] * len(info_data_id)
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S3_2_new[i].append(float(a[i]) * float(S3_1_new1[i][j]) + (1 - float(a[i])) * float(S3_2[i][j]))
                else:
                    S3_2_new[i].append(float(a[i]) * float(S3_1_new1[i][j]) + (1 - float(a[i])) * float(
                        S3_2_new[i][j - 1]))  ##计算二次指数的值
            S3_2_new1.append(S3_2_new[i])

        ##下面是计算二次指数平滑的值
        S3_3_new1 = []
        info_MSE = []  ##计算均方误差来得到最优的a(阿尔法)
        for i in range(0, len(info_data_sales)):
            S3_3_new = [[]] * len(info_data_id)
            MSE = 0
            for j in range(0, len(info_data_sales[i])):
                if j == 0:
                    S3_3_new[i].append(float(a[i]) * float(S3_2_new1[i][j]) + (1 - float(a[i])) * float(S3_3[i][j]))
                else:
                    S3_3_new[i].append(float(a[i]) * float(S3_2_new1[i][j]) + (1 - float(a[i])) * float(
                        S3_3_new[i][j - 1]))  ##计算三次指数的值
                MSE = (int(S3_3_new[i][j]) - int(info_data_sales[i][j])) ** 2 + MSE
            MSE = (MSE ** (1 / 2)) / int(len(info_data_sales[i]))
            info_MSE.append(MSE)
            S3_3_new1.append(S3_3_new[i])
            # print(S3_3_new1)

        ##下面是计算At、Bt、Ct以及每个预估值Xt的值，直接计算预估值，不一一列举Xt的值了
        u = input('你要预估多少期？')
        Xt = []
        for i in range(0, len(info_data_sales)):
            At = (
            float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) * 3 - float(S3_2_new1[i][len(S3_2_new1[i]) - 1]) * 3 + float(
                S3_3_new1[i][len(S3_3_new1[i]) - 1]))
            Bt = ((float(a[i]) / (2 * ((1 - float(a[i])) ** 2))) * ((6 - 5 * float(a[i])) * (
            float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) - 2 * (5 - 4 * float(a[i])) * float(
                S3_2_new1[i][len(S3_2_new1[i]) - 1]) + (4 - 3 * float(a[i])) * float(
                S3_3_new1[i][len(S3_3_new1[i]) - 1]))))
            Ct = (((float(a[i])) ** 2) / (2 * ((1 - float(a[i])) ** 2))) * (
            float(S3_1_new1[i][len(S3_1_new1[i]) - 1]) - float(S3_2_new1[i][len(S3_2_new1[i]) - 1])*2 + float(
                S3_3_new1[i][len(S3_3_new1[i]) - 1]))
            Xt.append(At + Bt * int(u) + Ct * (int(u) ** 2))
            print('第' + str(i + 1) + '组的三次平滑预估值为:' + str(Xt[i]) + '；均方误差为：' + str(info_MSE[i]))

---

以上，为本人从其他地方转来的，忘记了源地址，经本人验证，以上方法所预测的代码对很短时间内的预测有较强效果，但预测结果并没有R语言的预测结果，有可能是因为数据原因，在此不对原因进行深挖，最终使用python+R的方式进行了数据预测。以上代码对平滑预测法的算法会有些理解。