根据经纬度以及距离求周边正方形区间

1、概念

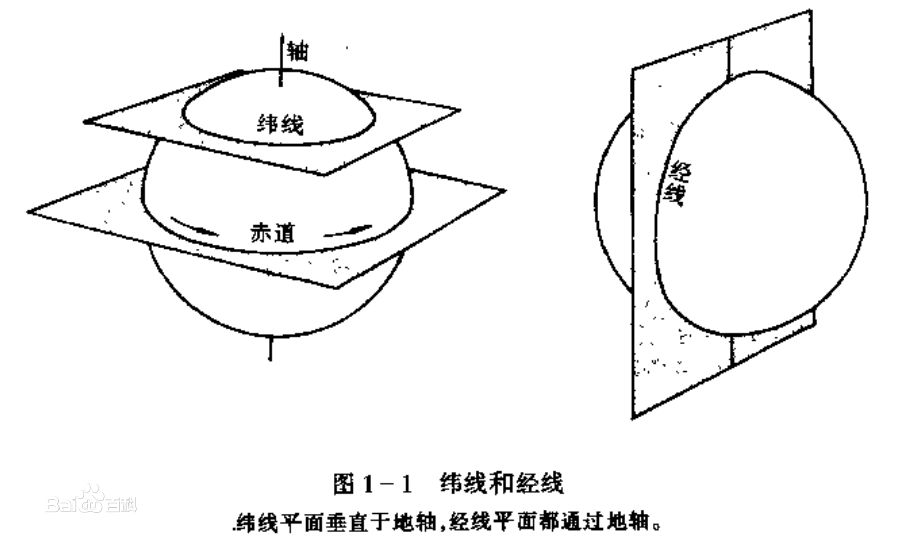
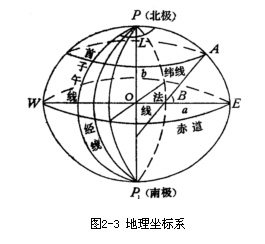
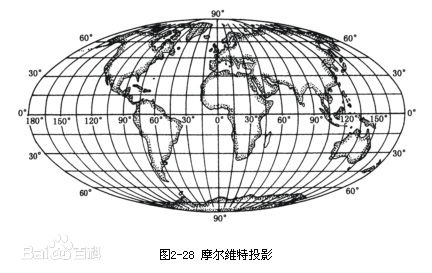
纬线、经线、维度、经度

2、根据两点的经纬度，计算距离

/**
     * <p>Description: 计算两点之间距离</p>
     * @param slng 起始经度
     * @param slat 起始纬度
     * @param elng 结束经度
     * @param elat 结束纬度
     * @return 米
     */
    public static double getDistanceByGaoDe(double slng, double slat, double elng, double elat) {
        double lng1 = (Math.PI / 180) * slng;
        double lng2 = (Math.PI / 180) * elng;
        double lat1 = (Math.PI / 180) * slat;
        double lat2 = (Math.PI / 180) * elat;

        // 两点间距离 km，如果想要米的话，结果*1000就可以了
        double d = Math.acos(
                Math.sin(lat1) * Math.sin(lat2) 
                + Math.cos(lat1) * Math.cos(lat2) * Math.cos(lng2 - lng1)
            ) * EARTH_RADIUS;
        // 精度1位小数
        d = Math.round(d * 10000d) / 10000d;
        
        return d * 1000;
    }

3、根据当前经纬度以及距离，求周边正方形区间（通过求出的区间范围作为SQL入参过滤数据）

/**
     * <p>Description: 计算两点之间距离</p>
     * @param dis 距离
     * @param lng 起始经度
     * @param lat 起始纬度
     * @return 正方形范围
     */
    public static double[] getPoiRange(double dis, double lng, double lat) {
        double[] poi = new double[4];
        
        double lng1 = (Math.PI / 180) * lng;
        double lng2 = (Math.PI / 180) * lng;
        double lat1 = (Math.PI / 180) * lat;
        double lat2 = (Math.PI / 180) * lat;
        
        // 角度
        double theta = dis / EARTH_RADIUS;
        
        // 维度相同，反算经度
        double lngVal = Math.cos(theta) - Math.sin(lat1) * Math.sin(lat2);
        double lngThetaVal = lngVal / (Math.cos(lat1) * Math.cos(lat2));
        double elng1 = (-Math.acos(lngThetaVal) + lng1) / (Math.PI / 180);
        double elng2 = (Math.acos(lngThetaVal) + lng1) / (Math.PI / 180);
        
        LogLIB.LogRun.info("elng1=" + UtilTools.format(elng1) + " elng2=" + UtilTools.format(elng2));
        
        // 经度相同，反算维度（根据辅助角公式计算 asinx + bcosx）
        // theta = a * Math.sin(lat2) + b * Math.cos(lat2) = Math.sqrt(a平方 + b平方)sin(x + arctan(b/a))
        double a = Math.sin(lat1);
        double b = Math.cos(lat1) * Math.cos(lng2 - lng1);
        double sqrt = Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2));
        double latTheteVal = Math.cos(theta) / sqrt;
        double elat1 = (Math.asin(latTheteVal) - Math.atan(b/a)) / (Math.PI / 180);
        double elat2 = (Math.asin(-latTheteVal) - Math.atan(b/a)) / (Math.PI / 180) + 180;
        
        LogLIB.LogRun.info("elat1=" + UtilTools.format(elat1) + " elat2=" + UtilTools.format(elat2));
        
        poi[0] = elng1;
        poi[1] = elng2;
        poi[2] = elat1;
        poi[3] = elat2;
        
        return poi;
    }